
分析 (1)对f(x)求导,对导函数中m进行分类讨论,由此得到单调区间,
(2)借助(1),对m进行分类讨论,由最大值小于等于0,构造新函数,转化为最值问题.
解答 解:(1)${f}^{′}(x)=\frac{1}{x}-\frac{m}{{x}^{2}}$ (x∈(0,+∞)),
当m≤0时,f′(x)>0恒成立,则函数f(x)在(0,+∞)上单调递增
此时函数f(x)的单调递增区间为(0,+∞),无单调递减区间;
当m>0时,令f′(x)>0,解得:x>m,令f′(x)<0,解得:0<x<m,
∴f(x)在(0,m)递减,在(m,+∞)递增;
(2)由(1)得:m≤0时,f(x)在(0,+∞)递增,
而f(1)=0,故f(x)<0在(0,1)成立,不合题意,
m>0时,f(x)在(0,m)递减,在(m,+∞)递增,
f(x)min=f(m)=1-m+lnm=0,解得:m=1.
点评 本题考查函数求导,分类讨论,构造新函数,将不等式转化为最值问题,是一道中档题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{8}{3}$,$\frac{28}{5}$) | B. | ($\frac{8}{3}$,$\frac{28}{5}$] | C. | ($\frac{8}{3}$,$\frac{18}{5}$) | D. | ($\frac{8}{3}$,$\frac{18}{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
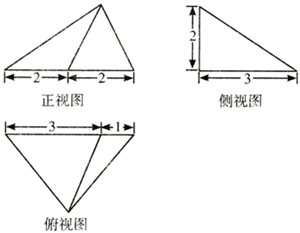
| A. | 12m3 | B. | $\frac{8}{3}{m^3}$ | C. | 4m3 | D. | 8m3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≤1 | B. | 0<m≤1 | C. | 0≤m≤1 | D. | m≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com