Question

在同一坐标系中，作出函数y=2sinx,y=sin2x，y=sin(x+)的图象.

Answer 1

解析：先分别用“五点法”作出长度为一个周期的区间上的简图.

通过列表可求得y=2sinx,x∈［0,2π］的五点坐标分别是（0，0），（,2）,(π,0),(,-2),(2π,0).

y=sin2x,x∈［0,π］的五点坐标分别是(0,0),(,1),(,0)，(,-1),(π,0).

y=sin(x+),x∈［-,］的五点坐标分别是(-,0),(,1),(,0),(,-1),(,0).

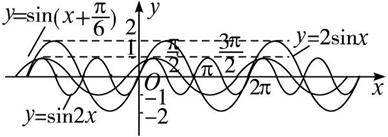
描点作图象，然后将函数y=2sinx在［0,2π］上的图象向左、右平移2kπ(k∈N^*)个单位，得到y=2sinx的图象.

将函数y=sin2x在［0,π］上的图象向左、右平移kπ(k∈N^*)个单位，得到y=sin2x的图象.

将函数y=sin(x+)在［-,］上的图象向左、右平移2kπ(k∈N^*)个单位，得到y=sin(x+)的图象（如上图）.

点评：在同一坐标系中作两个或三个函数图象，便于比较图象特征.