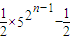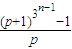(1)定义:若数列{dn}满足dn+1=dn2,则称{dn}为“平方递推数列”.已知:数列{an}中,a1=2,an+1=2an2+2an.
①求证:数列{2an+1}是“平方递推数列”;
②求证:数列{lg(2an+1)}是等比数列;
③求数列{an}的通项公式.
(2)已知:数列{bn}中,b1=1,bn+1=p2bn3+3pbn2+3bn(p>0),求:数列{bn}的通项.
【答案】
分析:(1)①依据“平方递推数列”定义,结合条件a
n+1=2a
n2+2a
n,可证数列{2a
n+1}是“平方递推数列”,
②令b
n=2a
n+1,进而有lgbn+1=2lgbn.从而可证数列{lgbn}为等比数列;
③由②知,数列{lg(2a
n+1)}是以lg5为首项,2为公比的等比数列,故可求
(2)两边同乘以p整理得,pb
n+1+1=(pb
n+1)
3,两边取对数得:lg(pb
n+1+1)=3lg(pb
n+1),故数列{lg(pb
n+1)}是以lg(p+1)为首项,3为公比的等比数列,从而可求数列{b
n}的通项.
解答:解:(1)①由条件a
n+1=2a
n2+2a
n,得2a
n+1+1=4a
n2+4a
n+1=(2a
n+1)
2.
∴数列{2a
n+1}是“平方递推数列”;
②令b
n=2a
n+1,∴b
n+1=2a
n+1+1.则lgb
n+1=2lgb
n.
∵lg(2a
1+1)=lg5≠0,∴
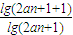
=2.
数列{lg(2a
n+1)}是等比数列;
③由②知,lg(2a
n+1)=
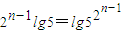
,∴2a
n+1=
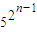
,∴a
n=
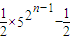
(2)两边同乘以p得,pb
n+1=p
3b
n3+3p
2b
n2+3pb
n(p>0),
∴pb
n+1+1=p
3b
n3+3p
2b
n2+3pb
n+1=(pb
n+1)
3,
两边取对数得:lg(pb
n+1+1)=3lg(pb
n+1)
∴数列{lg(pb
n+1)}是以lg(p+1)为首项,3为公比的等比数列
∴lg(pb
n+1)=3
n-1lg(p+1)
∴b
n=
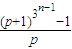 点评:
点评:本题的考点是数列递推式,主要考查新定义,将数列放到新情境中,关键是正确理解题意,挖掘问题的本质与隐含,解题时应注意构造新数列,从而使问题得解.

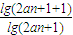 =2.
=2.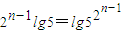 ,∴2an+1=
,∴2an+1=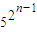 ,∴an=
,∴an=