
-![]() ��-1��0.
��-1��0.
(1)��aΪ��ֵʱ��a4=0.
(2)������{bn}����b1=-1,bn+1=![]() (n��N*).��֤aȡ����{bn}�е���һ���������Եõ�һ����������{an}.
(n��N*).��֤aȡ����{bn}�е���һ���������Եõ�һ����������{an}.
(3)��![]() ��an��2(n��4),��a��ȡֵ��Χ.
��an��2(n��4),��a��ȡֵ��Χ.
������(1)��a4=0,��1+![]() =0,��a3=-1.
=0,��a3=-1.
��a3=1+![]() ,��a2=-
,��a2=-![]() .
.
��a2=1+![]() ,��a=-
,��a=-![]() .
.
�ʵ�a=-![]() ʱ��a4=0.
ʱ��a4=0.
(2)��b1=-1,bn+1=![]() ,��bn=
,��bn=![]() +1.
+1.
aȡ����{bn}�е���һ������������a=bn,
��a=bn,��a2=1+![]() =1+
=1+![]() =bn-1,
=bn-1,
��a3=1+![]() =1+
=1+![]() =bn-2,
=bn-2,
��
��an=1+![]() =1+
=1+![]() =b1=-1,
=b1=-1,
��an+1=0.
��aȡ����{bn}�е���һ�����������Եõ�һ����������{an}.
(3)Ҫʹ![]() ��an��2,��
��an��2,��![]() ��1+
��1+![]() ��2,
��2,
��1��an-1��2,
��Ҫʹ![]() ��an��2,���ҽ�������ǰһ��an-1����1��an-1��2.
��an��2,���ҽ�������ǰһ��an-1����1��an-1��2.
�ߣ�![]() ,2��
,2��![]() (1,2),
(1,2),
��ֻ�뵱a4��(![]() ,2)ʱ������an��(
,2)ʱ������an��(![]() ,2) (n��5).
,2) (n��5).
��a4=![]() �ã�
�ã�![]() ��
��![]() ��2.
��2.
�ⲻ��ʽ��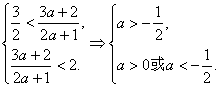
��a��0.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3+4an |
| 12-4an |
| 1 | ||
an-
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 |
| 2 |
| 3nan-1 |
| 2an-1+n-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 5 | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com