
分析 ①依题意,可得0<$\frac{a}{c}$<1,0<$\frac{b}{c}$<1,故当x∈(-∞,1)时,f(x)=cx[${(\frac{a}{c})}^{x}$+${(\frac{b}{c})}^{x}$-1]>cx($\frac{a}{c}$+$\frac{b}{c}$-1)=cx•$\frac{a+b+c}{c}$>0,可判断①正确;
②令a=2,b=3,c=4,则a,b,c可以构成三角形的三边长,但a2=4,b2=9,c2=16却不能构成三角形的三边长,可判断②正确;
③由c>a>0,c>b>0,且△ABC为钝角三角形,可知a2+b2-c2<0,故f(1)=a+b-c>0,f(2)=a2+b2-c2<0,利用零点存在定理可判断③正确;
④若△ABC为直角三角形,则c2=a2+b2,对于n∈N*,f(2n)=a2n+b2n-c2n=a2n+b2n-(a2+b2)n≤0,可判断④不正确.
解答 解:①因为a,b,c是三角形的三条边长,所以a+b>c,又因为c>a>0,c>b>0,所以0<$\frac{a}{c}$<1,0<$\frac{b}{c}$<1,所以当x∈(-∞,1)时,f(x)=cx[${(\frac{a}{c})}^{x}$+${(\frac{b}{c})}^{x}$-1]>cx($\frac{a}{c}$+$\frac{b}{c}$-1)=cx•$\frac{a+b-c}{c}$>0,故①正确;
②令a=2,b=3,c=4,则a,b,c可以构成三角形的三边长,但a2=4,b2=9,c2=16却不能构成三角形的三边长,故②正确;
③因为c>a>0,c>b>0,且△ABC为钝角三角形,所以a2+b2-c2<0,于是f(1)=a+b-c>0,f(2)=a2+b2-c2<0,故函数f(x)在区间(1,2)内存在零点,即?x0∈(1,2),使f(x0)=0,故③正确;
④若△ABC为直角三角形,由题意得,c2=a2+b2,对于n∈N*,f(2n)=a2n+b2n-c2n=a2n+b2n-(a2+b2)n≤0,故④不正确.
综上,正确结论的序号为①②③.
故答案为:①②③.
点评 本题考查命题的真假判断与应用,着重考查在条件c>a>0,c>b>0下,函数f(x)=ax+bx-cx的性质的应用,考查转化思想与综合运用能力,属于难题.


 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
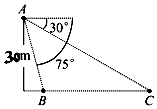 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是30m,则河流的宽度BC等于$60(\sqrt{3}-1)$m.
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是30m,则河流的宽度BC等于$60(\sqrt{3}-1)$m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com