
A.x-3y+2=0(x≠1) B.3x-y-2=0(x≠1)
C.3x+y-4=0(x≠1) D.3x-y-1=0(x≠1)
科目:高中数学 来源: 题型:
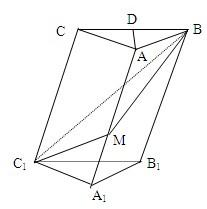 在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.
在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| c |
| ||
| 7 |
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| a |
| c |
| b |
| c |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
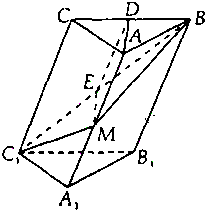 在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.
在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| c |
| ||
| 7 |
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| a |
| c |
| b |
| c |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京大学附中高三(上)数学练习试卷4(文科)(解析版) 题型:填空题
 与
与 都是非零向量,则“
都是非零向量,则“ ”是“
”是“ ”的充要条件;②已知等腰△ABC的腰为底的2倍,则顶角A的正切值是
”的充要条件;②已知等腰△ABC的腰为底的2倍,则顶角A的正切值是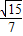 ;③在平面直角坐标系xoy中,四边形ABCD的边AB∥DC,AD∥BC,已知点A(-2,0),B(6,8),C(8,6),则D点的坐标为(0,-1);④设
;③在平面直角坐标系xoy中,四边形ABCD的边AB∥DC,AD∥BC,已知点A(-2,0),B(6,8),C(8,6),则D点的坐标为(0,-1);④设 ,
, ,
, 为同一平面内具有相同起点的任意三个非零向量,且满足
为同一平面内具有相同起点的任意三个非零向量,且满足 与
与 不共线,
不共线, ⊥
⊥ ,|
,| |=|
|=| |,则|
|,则| •
• |的值一定等于以
|的值一定等于以 ,
, 为邻边的平行四边形的面积.其中正确命题的序号是 .(写出全部正确结论的序号)
为邻边的平行四边形的面积.其中正确命题的序号是 .(写出全部正确结论的序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com