
【题目】如图所示,在四棱锥P-ABCD中,四边形ABCD为平行四边形,△PCD为正三角形,∠BAD=30°,AD=4,AB=2![]() ,平面PCD⊥平面ABCD,E为PC中点.
,平面PCD⊥平面ABCD,E为PC中点.
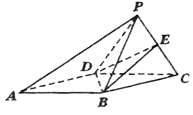
(1)证明:BE⊥PC;
(2)求多面体PABED的体积.
【答案】(1)见解析;(2)3![]()
【解析】
(1)先证明PC⊥面BDE,再证明BE⊥PC;
(2)先求![]() 的体积,再求
的体积,再求![]() 的体积,从而可得多面体PABED的体积.
的体积,从而可得多面体PABED的体积.
(1)∵BD2=AB2+AD2![]() 2ABADcos∠BAD=4,∴BD=2,
2ABADcos∠BAD=4,∴BD=2,
∴∠ABD=90°,∴BD⊥CD,∵面PCD⊥面ABCD,面PCD∩面ABCD=CD,
∴BD⊥面PCD,∴BD⊥PC,∵△PCD是正三角形,E为PC的中点,∴DE⊥PC,
∴PC⊥面BDE,∴BE⊥PC.
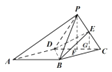
(2)作PF⊥CD,EG⊥CD,F,G为垂足,∵面PCD⊥面ABCD,
∴PF⊥面ABCD,EG⊥面ABCD,∵△PCD是正三角形,CD=2![]() ,
,
∴PF=3,EG=![]() ,∴VP-ABCD=
,∴VP-ABCD=![]() =4
=4![]() ,
,
![]() =
=![]() ,
,
∴多面体PABED的体积V=VP-ABCD-VE-BCD=4![]() =3
=3![]() .
.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】如图,2012年春节,摄影爱好者S在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为![]() ,已知S的身高约为
,已知S的身高约为![]() 米(将眼睛距地面的距离按
米(将眼睛距地面的距离按![]() 米处理)
米处理)
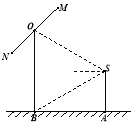
(1) 求摄影者到立柱的水平距离和立柱的高度;
(2) 立柱的顶端有一长2米的彩杆MN绕中点O在S与立柱所在的平面内旋转.摄影者有一视角范围为![]() 的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
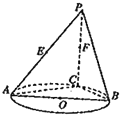
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设(1)中的直线l与圆O的另一个交点为D,且点Q满足![]() .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校组织高一、高二年级学生进行了“纪念建国70周年”的知识竞赛.从这两个年级各随机抽取了40名学生,对其成绩进行分析,得到了高一年级成绩的频率分布直方图和高二年级成绩的频数分布表.
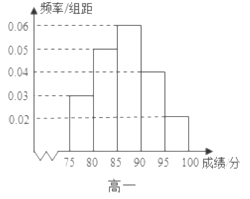
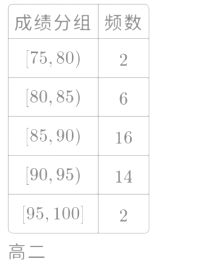
(Ⅰ)若成绩不低于80分为“达标”,估计高一年级知识竞赛的达标率;
(Ⅱ)在抽取的学生中,从成绩为[95,100]的学生中随机选取2名学生,代表学校外出参加比赛,求这2名学生来自于同一年级的概率;
(Ⅲ)记高一、高二两个年级知识竞赛的平均分分别为![]() ,试估计
,试估计![]() 的大小关系.(只需写出结论)
的大小关系.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改革”引起广泛关注,为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3 000人进行调查,就“是否取消英语听力”问题进行了问卷调查统计,结果如下表:
态度 | |||
调查人群 | 应该取消 | 应该保留 | 无所谓 |
在校学生 | 2100人 | 120人 | y人 |
社会人士 | 500人 | x人 | z人 |
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.06.
(1)现用分层抽样的方法在所有参与调查的人中抽取300人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取6人,然后从这6人中随机抽取2人,求这2人中恰好有1个人为在校学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为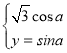 ,(a为参数)。以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为
,(a为参数)。以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为![]() ,将C2逆时针旋转
,将C2逆时针旋转![]() 以后得到曲线C3.
以后得到曲线C3.
(1)写出C1与C3的极坐标方程;
(2)设C2与C3分别交曲线C1于A、B和C、D四点,求四边形ACBD面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com