
【题目】已知函数![]() 有两个零点
有两个零点![]() ,
,![]() ,则下列判断:①
,则下列判断:①![]() ;②
;②![]() ;③
;③![]() ;④有极小值点
;④有极小值点![]() ,且
,且![]() .则正确判断的个数是( )
.则正确判断的个数是( )
A. 4个B. 3个C. 2个D. 1个
【答案】D
【解析】
对函数求导得到函数的极值点进而得到a>e,①不正确,先由函数单调性得到④正确,再推断②③的正误.
对函数求导:当a≤0时,f′(x)=ex﹣a>0在x∈R上恒成立,
∴f(x)在R上单调递增.
当a>0时,∵f′(x)=ex﹣a>0,∴ex﹣a>0,解得x>lna,
∴f(x)在(﹣∞,lna)单调递减,在(lna,+∞)单调递增.
∵函数f(x)=ex﹣ax有两个零点x1<x2,
∴f(lna)<0,a>e,
∴elna﹣alna<0,∴a>e,①不正确;
![]()
函数的极小值点为![]()
要证![]() ,只要证
,只要证![]()
因为函数f(x)在(﹣∞,![]() )单调递减,故只需要证
)单调递减,故只需要证![]()
构造函数![]()
![]()
求导得到![]()
所以函数![]() 单调递增,
单调递增,![]() 恒成立,
恒成立,
![]() 即
即![]() ,故得到
,故得到![]()
进而得证:![]() ,
,![]() .故④正确.
.故④正确.
又因为
根据![]() ,可得到
,可得到![]() .③不正确.
.③不正确.
因为![]() 故②
故②![]() 不确定.综上正确的只有一个.
不确定.综上正确的只有一个.
故答案为:D.


科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,四边形ABCD为平行四边形,△PCD为正三角形,∠BAD=30°,AD=4,AB=2![]() ,平面PCD⊥平面ABCD,E为PC中点.
,平面PCD⊥平面ABCD,E为PC中点.
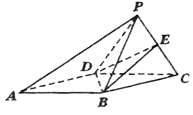
(1)证明:BE⊥PC;
(2)求多面体PABED的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :坐标系与参数方程选讲.
:坐标系与参数方程选讲.
在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ),曲线
),曲线![]()
![]() (
(![]() 为参数,实数
为参数,实数![]() ). 在以
). 在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点. 当
两点. 当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
(1)求![]() 的值; (2)求
的值; (2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年“双十一”当天,甲、乙两大电商进行了打折促销活动,某公司分别调查了当天在甲、乙电商购物的1000名消费者的消费金额,得到了消费金额的频数分布表如下:
甲电商:
消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
频数 | 50 | 200 | 350 | 300 | 100 |
乙电商:
消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
频数 | 250 | 300 | 150 | 100 | 200 |
(Ⅰ)根据频数分布表,完成下列频率分布直方图,并根据频率分布直方图比较消费者在甲、乙电商消费金额的中位数的大小以及方差的大小(其中方差大小给出判断即可,不必说明理由);
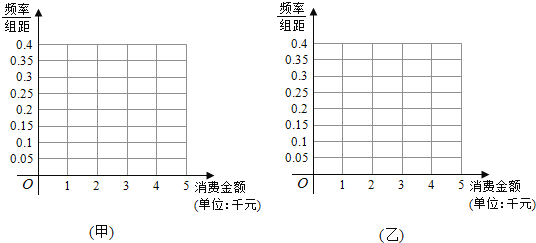
(Ⅱ)(ⅰ)根据上述数据,估计“双十一”当天在甲电商购物的大量的消费者中,消费金额小于3千元的概率;
(ⅱ)现从“双十一”当天在甲电商购物的大量的消费者中任意调查5位,记消费金额小于3千元的人数为X,试求出X的期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为6,离心率为
的长轴长为6,离心率为![]() .
.
(1)求椭圆C的标准方程;
(2)设椭圆C的左右焦点分别为![]() ,
,![]() ,左右顶点分别为A,B,点M,N为椭圆C上位于x轴上方的两点,且
,左右顶点分别为A,B,点M,N为椭圆C上位于x轴上方的两点,且![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,记直线AM,BN的斜率分别为
,记直线AM,BN的斜率分别为![]() ,试证明:
,试证明:![]() 的值为定值.
的值为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 过点
过点![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆C的标准方程;
(2)设F1,F2分别为椭圆C的左、右焦点,过F2的直线l与椭圆C交于不同两点M,N,记△F1MN的内切圆的面积为S,求当S取最大值时直线l的方程,并求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com