练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

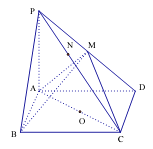
    【题目】在四棱锥中，底面是矩形， 平面， ，以的中点为球心， 为直径的球面交于点，交于点.

    （1）求证：平面平面；

    （2）求点到平面的距离.

    【答案】（1）见解析 （2）

    【解析】试题分析：（1）先根据等腰三角形性质得,再由平面得,又由矩形得AD ,根据线面垂直判定定理得平面,即得，再根据线面垂直判定定理得平面，最后根据面面垂直判定定理得平面平面（2）求点到平面距离一般转化为求对应三棱锥的高，利用等体积法求体积，再根据体积公式求结果

    试题解析：（1）易得平面，所以平面平面（2）由

    所以点到平面的距离为

    点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.

    (1)证明线面、面面平行，需转化为证明线线平行.

    (2)证明线面垂直，需转化为证明线线垂直.

    (3)证明线线垂直，需转化为证明线面垂直.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=Asin（ωx﹣ ）（A＞0，ω＞0）的最大值为2，其图象相邻两条对称轴之间的距离为 ． （Ⅰ）求函数f（x）的最小正周期及解析式；
    （Ⅱ）求函数f（x）的单调减区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足an+1=a ﹣nan+1，且a1=2．
    （1）计算a2 ， a3 ， a4的值，由此猜想数列{an}的通项公式，并用数学归纳法证明；
    （2）求证：2nn≤a ＜3nn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 的图象过点（﹣1，2），且在点（﹣1，f（﹣1））处的切线与直线x﹣5y+1=0垂直．
    （1）求实数b，c的值；
    （2）求f（x）在[﹣1，e]（e为自然对数的底数）上的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆E： =1（a＞b＞0）上任意一点到两焦点距离之和为 ，离心率为 ，左、右焦点分别为F1 ， F2 ， 点P是右准线上任意一点，过F2作直线PF2的垂线F2Q交椭圆于Q点．
    （1）求椭圆E的标准方程；
    （2）证明：直线PQ与直线OQ的斜率之积是定值；
    （3）证明：直线PQ与椭圆E只有一个公共点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a＞0，a≠1且loga3＞loga2，若函数f（x）=logax在区间[a，2a]上的最大值与最小值之差为1．
    （1）求a的值；
    （2）解不等式 ；
    （3）求函数g（x）=|logax﹣1|的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=（ + ）x3（a＞0，a≠1）．
    （1）讨论函数f（x）的奇偶性；
    （2）求a的取值范围，使f（x）+f（2x）＞0在其定义域上恒成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

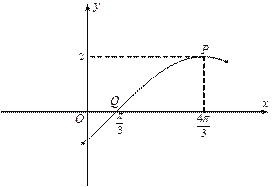
    【题目】如图为函数图像的一部分，其中点是图像的一个最高点，点是与点相邻的图像与轴的一个交点.

    ⑴ 求函数的解析式；

    ⑵ 若将函数的图像沿轴向右平移个单位，再把所得图像上每一点的横坐标都变为原来的（纵坐标不变），得到函数的图像，求函数的单调递增区间.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2013年第三季度，国家电网决定对城镇居民用电计费标准作出调整，并根据用电情况将居民分为三类：第一类的用电区间在（0，170]，第二类在（170，260]，第三类在（260，+∞）（单位：千瓦时）．某小区共有1000户居民，现对他们的用电情况进行调查，得到频率分布直方图，如图所示．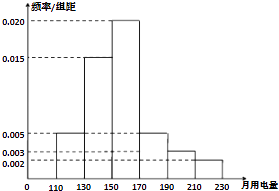

    （1）求该小区居民用电量的中位数与平均数；
    （2）本月份该小区没有第三类的用电户出现，为鼓励居民节约用电，供电部门决定：对第一类每户奖励20元钱，第二类每户奖励5元钱，求每户居民获得奖励的平均值；
    （3）利用分层抽样的方法从该小区内选出5位居民代表，若从该5户居民代表中任选两户居民，求这两户居民用电资费属于不同类型的概率．

    查看答案和解析>>

    同步练习册答案