
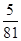 ;(2)分布列详见解析,
;(2)分布列详见解析,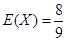 .
.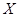 有4种情况:当
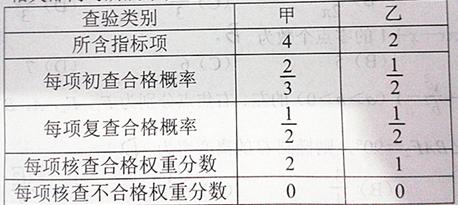
有4种情况:当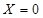 时,表示既没有奖励又没有罚款的情况,也就是第一问的情况;当
时,表示既没有奖励又没有罚款的情况,也就是第一问的情况;当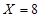 时,表示累计权重分数为9分,也就是甲的4个指标项都合格,而乙中的2个指标项只有1个合格;当
时,表示累计权重分数为9分,也就是甲的4个指标项都合格,而乙中的2个指标项只有1个合格;当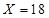 时,表示累计权重分数为10分,也就是说甲乙中的所以指标项都合格的情况;当
时,表示累计权重分数为10分,也就是说甲乙中的所以指标项都合格的情况;当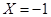 时,表示累计权重分数为7分,也就是甲中的4个指标项有3个合格1个不合格,乙中的2个指标项1个合格1个不合格,利用分析的情况列出概率表达式,列出分布列,利用期望的计算公式求数学期望.
时,表示累计权重分数为7分,也就是甲中的4个指标项有3个合格1个不合格,乙中的2个指标项1个合格1个不合格,利用分析的情况列出概率表达式,列出分布列,利用期望的计算公式求数学期望.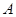 ,“初查阶段乙类的一个指标项合格”为事件
,“初查阶段乙类的一个指标项合格”为事件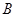 ,“复查阶段一个指标项合格”为事件
,“复查阶段一个指标项合格”为事件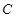 ,则
,则 ,
,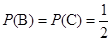 .
. ,则
,则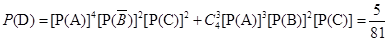 . 4分
. 4分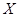 的可能取值为-1,0,8,18.
的可能取值为-1,0,8,18.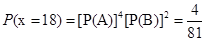 ,
,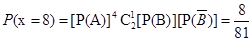 ,
,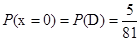 ,
,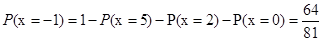 .
.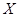 的分布列为
的分布列为| X | -1 | 0 | 8 | 18 | |
| P | 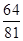 | 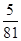 | 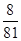 | 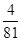 | 10分 |
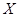 的数学期望
的数学期望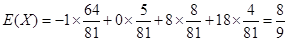 (万元). 12分
(万元). 12分

科目:高中数学 来源:不详 题型:解答题
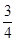 ,
,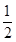 ,
,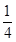 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 鱼的 质量 | [1.00, 1.05) | [1.05, 1.10) | [1.10, 1.15) | [1.15, 1.20) | [1.20, 1.25) | [1.25, 1.30) |
| 鱼的 条数 | 3 | 20 | 35 | 31 | 9 | 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.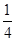 | B. | C.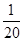 | D.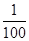 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.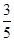 ; ; | B.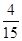 ; ; | C.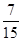 ; ; | D. . . |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com