解:(1)由已知,2S
n=a
n2+a
n-2(n∈N
*)①
得:a
1=2,a
2=3,a
3=4,…(2分)
又2S
n+1=a
n+12+a
n+1-2②
由②-①得; (a
n+1-a
n-1)(a
n+1+a
n)=0,(a
n>0)
即a
n+1-a
n=1(n≥2,n∈N
*),且a
2-a
1=1.
∴数列{a
n}是以a
1=2为首项,公差为1的等差数列.
∴a
n=n+1. …(4分)
(2)由(Ⅰ)知b
n=(n+1)•2
n它的前n项和为T
n,
T
n=2•2
1+3•2
2+4•2
3+…+n•2
n-1+(n+1)•2
n ①
2T
n=2•2
2+3•2
3+4•2
4+…+n•2
n+(n+1)•2
n+1 ②
①-②:-T
n=2•2
1+2
2+2
3+2
4+…+2
n-(n+1)•2
n+1=

=-n•2
n+1∴T
n=n•2
n+1…(8分)…(6分)
(3)∵a
n=n+1,∴c
n=4
n+(-1)
n-1λ•2
n+1,
要使c
n+1>c
n恒成立,
∴c
n+1-c
n=4
n+1-4
n+(-1)
nλ•2
n+2-(-1)
n-1λ•2
n+1>0恒成立
∴3•4
n-3λ•(-1)
n-12
n+1>0恒成立,
∴(-1)
n-1λ<2
n-1恒成立. …(9分)
(ⅰ)当n为奇数时,即λ<2
n-1恒成立
当且仅当n=1时,2
n-1有最小值为1,
∴λ<1.…(11分)
(ⅱ)当n为偶数时,即λ>-2
n-1恒成立
当且仅当n=2时,-2
n-1有最大值-2,
∴λ>-2.…(13分)
即-2<λ<1,又λ为非零整数,则λ=-1.
综上所述,存在λ=-1,使得对任意n∈N
*,
都有c
n+1>c
n.…(14分)
分析:(1)由2S
n=a
n2+a
n-2(n∈N
*),得:a
1=2,a
2=3,a
3=4,又2S
n+1=a
n+12+a
n+1-2,故a
n+1-a
n=1(n≥2,n∈N
*),且a
2-a
1=1.由此能求出{a
n}的通项公式.
(2)由b
n=(n+1)•2
n,其前n项和T
n=2•2
1+3•2
2+4•2
3+…+n•2
n-1+(n+1)•2
n,由错位相减法能求出T
n.
(3)由a
n=n+1,知c
n=4
n+(-1)
n-1λ•2
n+1,要使c
n+1>c
n恒成立,则c
n+1-c
n=4
n+1-4
n+(-1)
nλ•2
n+2-(-1)
n-1λ•2
n+1>0恒成立,故(-1)
n-1λ<2
n-1恒成立. 由此能得到存在λ=-1,使得对任意n∈N
*,都有c
n+1>c
n.
点评:本题考查数列与不等式的综合,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.易错点是计算繁琐,容易失误.解题时要认真审题,仔细解答.

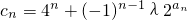 (λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,有cn+1>cn恒成立.
(λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,有cn+1>cn恒成立.


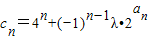 (λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,有cn+1>cn恒成立.
(λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,有cn+1>cn恒成立.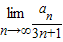 = .
= .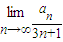 = .
= .