
分析 (Ⅰ)由$\frac{x+1}{x-1}$>0解得定义域,在定义域范围内考察f(-x)=-f(x)成立;
(Ⅱ)根据对数的性质,转化为真数大小关系恒成立,再利用分离参数法求m范围.
解答 解 (Ⅰ)由 $\frac{x+1}{x-1}$>0,解得x<-1或x>1,
∴函数的定义域为(-∞,-1)∪(1,+∞),
当x∈(-∞,-1)∪(1,+∞)时,
f(-x)=loga $\frac{-x+1}{-x-1}$=loga $\frac{x-1}{x+1}$=-loga $\frac{x+1}{x-1}$=-f(x),
∴f(x)=loga $\frac{x+1}{x-1}$在定义域上是奇函数.
(2)由x∈[2,4]时,f(x)=loga $\frac{x+1}{x-1}$>loga $\frac{m}{(x-1)(7-x)}$恒成立,
①当a>1时,
∴$\frac{x+1}{x-1}$>$\frac{m}{(x-1)(7-x)}$对x∈[2,4]恒成立,
∴0<m<(x+1)(7-x)在x∈[2,4]恒成立,
设g(x)=(x+1)(7-x),x∈[2,4],
则g(x)=-x2+6x+7=-(x-3)2+16,
g(x)min=g(2)=g(4)=15,
∴0<m<15;
②当0<a<1时,由x∈[2,4]时,
f(x)=loga $\frac{x+1}{x-1}$>loga $\frac{m}{(x-1)(7-x)}$恒成立,
∴$\frac{x+1}{x-1}$<$\frac{m}{(x-1)(7-x)}$对x∈[2,4]恒成立,
∴m>(x+1)(7-x)在x∈[2,4]恒成立,
设g(x)=(x+1)(7-x),x∈[2,4],
由①得:g(x)max=g(3)=16,∴m>16,
∴m的取值范围是(0,15)∪(16,+∞).
点评 本题考查了函数奇偶性的判定,不等式恒成立问题,函数最值求解,考查运算求解能力.


科目:高中数学 来源: 题型:选择题
| A. | 定义域是[-1,1] | B. | f(x)是奇函数 | ||
| C. | 值域是[-tan1,tan1] | D. | 在(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
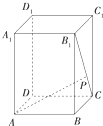 如图所示,在长方体ABCD-A1B1C1D1中,AB=2,AD=3,AA1=2$\sqrt{6}$,点P是B1C的三等分点且靠近点C,则异面直线AP和DD1所成的角为( )
如图所示,在长方体ABCD-A1B1C1D1中,AB=2,AD=3,AA1=2$\sqrt{6}$,点P是B1C的三等分点且靠近点C,则异面直线AP和DD1所成的角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{5π}{12}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com