Question

已知函数f （x）=-ax³+x²+（a-1）x-（x＞0），（a∈R）．
（Ⅰ）当0＜a＜时，讨论f （x）的单调性；
（Ⅱ）若f （x）在区间（a，a+1）上不具有单调性，求正实数a的取值范围．

Answer 1

解：（Ⅰ） f （x）的定义域为（0，+∞）．
由f （x）=-ax³+x²+（a-1）x-（x＞0），
得：f'（x）=-ax²+x+a-1=-a（x-1）[x-（-1）]．
当0＜a＜时，-1＞1，
∴当x∈（0，1）时，f'（x）=-a（x-1）[x-（-1）]＜0，
当x∈（-1，+∞）时，f'（x）=-a（x-1）[x-（-1）]＜0，
当x∈（1，-1）时，f'（x）=-a（x-1）[x-（-1）]＞0．
∴f （x）=-ax³+x²+（a-1）x-在（0，1），（-1，+∞）递减；在（1，-1）递增；
（Ⅱ） f （x）在区间（a，a+1）上不具有单调性等价于f （x）在区间（a，a+1）内至少有一个极值点．
①当a=时，f′（x）=-（x-1）²≤0?f （x）在（0，+∞）上递减，不合题意；
②当a≥1时，f′（x）=0的两根为x₁=1，x₂=-1，∵x₁，x₂∉（a，a+1），故不合题意；
③当0＜a＜1，且a≠时，f （x）在区间（a，a+1）上不具有单调性等价于：a＜1＜a+1或
解a＜1＜a+1得：0＜a＜1．
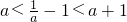
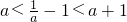解得：．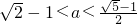
∵0＜a＜1，且a≠，∴0＜a＜1，且a≠．
综上可知，所求a的取值范围是（0，）∪（，1）．
分析：（Ⅰ）求出原函数的导函数，因式分解后根据a的范围判断导函数在（0，1）、（-1，+∞）、（1，-1）内的符号，从而得到原函数在这三个区间内的单调性；
（Ⅱ）f （x）在区间（a，a+1）上不具有单调性，等价于f （x）在区间（a，a+1）内至少有一个极值点．根据（Ⅰ）中求出的导函数，分a=、a≥1和0＜a＜1且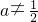三种情况讨论函数f （x）在区间（a，a+1）上的单调性及有极值时的a的范围．
点评：本题主要考查导函数的正负与原函数的单调性之间的关系，即当导函数大于0时原函数单调递增，当导函数小于0时原函数单调递减，考查了函数在给定区间内不是单调函数的条件及运用该条件求解参数取值范围的方法，此题属难题．