
【题目】已知圆C经过点A(﹣2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)若![]() ,求实数k的值;
,求实数k的值;
(3)过点(0,4)作动直线m交圆C于E,F两点.试问:在以EF为直径的所有圆中,是否存在这样的圆P,使得圆P经过点M(2,0)?若存在,求出圆P的方程;若不存在,请说明理由.
【答案】(1)x2+y2=4(2)k=0(3)存在圆P:5x2+5y2﹣16x﹣8y+12=0或x2+y2=4,使得圆P经过点M(2,0).
【解析】试题分析:(1)先求出AB中垂线方程,再与直线y=x联立求出交点即为圆心,最后根据圆心到A点距离等于半径,写出圆方程(2)联立直线y=kx+1与圆方程,根据向量数量积以及韦达定理化简可得实数k的值;(3)设E,F坐标,则可表示出以EF为直径的圆方程,再设直线m点斜式方程与圆C方程联立,利用韦达定理以及以EF为直径的圆过点M(2,0)求出直线m斜率,代入即得以EF为直径的圆方程,最后讨论直线m斜率不存在时是否满足题意
试题解析:解:(1)设圆心C(a,a),半径为r.
因为圆C经过点A(﹣2,0),B(0,2),
所以|AC|=|BC|=r,
即 ,
,
解得a=0,r=2,
所以圆C的方程是x2+y2=4.
(2)因为![]()
![]() =2×2×cos<
=2×2×cos<![]() ,
,![]() >=﹣2,
>=﹣2,
且![]() 与
与![]() 的夹角为∠POQ,
的夹角为∠POQ,
所以cos∠POQ=﹣![]() ,∠POQ=120°,
,∠POQ=120°,
所以圆心C到直线l:kx﹣y+1=0的距离d=1,
又d=![]() ,所以k=0.
,所以k=0.
(3)(ⅰ)当直线m的斜率不存在时,
直线m经过圆C的圆心C,
此时直线m与圆C的交点为E(0,2),F(0,﹣2),
EF即为圆C的直径,而点M(2,0)在圆C上,
即圆C也是满足题意的圆.
(ⅱ)当直线m的斜率存在时,设直线m:y=kx+4,
由![]() ,消去y整理,得(1+k2)x2+8kx+12=0,
,消去y整理,得(1+k2)x2+8kx+12=0,
由△=64k2﹣48(1+k2)>0,得![]() 或
或![]() .
.
设E(x1,y1),F(x2,y2),
则有 ①…
①…
由①得![]() ,②
,②![]() ,③
,③
若存在以EF为直径的圆P经过点M(2,0),则ME⊥MF,
所以![]() ,
,
因此(x1﹣2)(x2﹣2)+y1y2=0,
即x1x2﹣2(x1+x2)+4+y1y2=0,…
则![]() ,
,
所以16k+32=0,k=﹣2,满足题意.…
此时以EF为直径的圆的方程为x2+y2﹣(x1+x2)x﹣(y1+y2)y+x1x2+y1y2=0,
即![]() ,
,
亦即5x2+5y2﹣16x﹣8y+12=0.…
综上,在以EF为直径的所有圆中,
存在圆P:5x2+5y﹣16x﹣8y+12=0或x2+y2=4,使得圆P经过点M(2,0). …


科目:高中数学 来源: 题型:
【题目】京剧是我国的国粹,是“国家级非物质文化遗产”,某机构在网络上调查发现各地京剧票友的年龄![]() 服从正态分布
服从正态分布![]() 同时随机抽取
同时随机抽取![]() 位参与某电视台《我爱京剧》节目的票友的年龄作为样本进行分析研究(全部票友的年龄都在
位参与某电视台《我爱京剧》节目的票友的年龄作为样本进行分析研究(全部票友的年龄都在![]() 内),样本数据分别区间为
内),样本数据分别区间为![]() 由此得到如图所示的频率分布直方图.
由此得到如图所示的频率分布直方图.

(Ⅰ) 若![]() 求
求![]() 的值;
的值;
(Ⅱ)现从样本年龄在![]() 的票友中组织了一次有关京剧知识的问答,每人回答一个问题,答对赢得一台老年戏曲演唱机,答错没有奖品,假设每人答对的概率均为
的票友中组织了一次有关京剧知识的问答,每人回答一个问题,答对赢得一台老年戏曲演唱机,答错没有奖品,假设每人答对的概率均为![]() ,且每个人回答正确与否相互之间没有影响,用
,且每个人回答正确与否相互之间没有影响,用![]() 表示票友们赢得老年戏曲演唱机的台数,求
表示票友们赢得老年戏曲演唱机的台数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 上的点,
上的点,
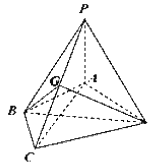
(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,求
的中点,求![]() 与平面
与平面![]() 所成的角的正切值;
所成的角的正切值;
(3)若![]() 满足
满足![]() 面
面![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函f(x)=sin(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示: 
(1)求ω,φ的值;
(2)设g(x)=2 ![]() f(
f( ![]() )f(
)f( ![]() )﹣1,当x∈[0,
)﹣1,当x∈[0, ![]() ]时,求函数g(x)的值域.
]时,求函数g(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】元旦期间,某轿车销售商为了促销,给出了两种优惠方案,顾客只能选择其中的一种,方案一:每满![]() 万元,可减
万元,可减![]() 千元;方案二:金额超过
千元;方案二:金额超过![]() 万元(含
万元(含![]() 万元),可摇号三次,其规则是依次装有
万元),可摇号三次,其规则是依次装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的一个摇号机,装有
个吉祥号的一个摇号机,装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的二号摇号机,装有
个吉祥号的二号摇号机,装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的三号摇号机各摇号一次,其优惠情况为:若摇出
个吉祥号的三号摇号机各摇号一次,其优惠情况为:若摇出![]() 个幸运号则打
个幸运号则打![]() 折,若摇出
折,若摇出![]() 个幸运号则打
个幸运号则打![]() 折;若摇出
折;若摇出![]() 个幸运号则打
个幸运号则打![]() 折;若没有摇出幸运号则不打折.
折;若没有摇出幸运号则不打折.
(1)若某型号的车正好![]() 万元,两个顾客都选中第二中方案,求至少有一名顾客比选择方案一更优惠的概率;
万元,两个顾客都选中第二中方案,求至少有一名顾客比选择方案一更优惠的概率;
(2)若你评优看中一款价格为![]() 万的便型轿车,请用所学知识帮助你朋友分析一下应选择哪种付款方案.
万的便型轿车,请用所学知识帮助你朋友分析一下应选择哪种付款方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是首项为a1=![]() ,公比q=
,公比q=![]() 的等比数列,设
的等比数列,设![]() ,数列
,数列![]() 满足cn=an·bn.
满足cn=an·bn.
(1)求证:{bn}是等差数列;
(2)求数列{cn}的前n项和Sn;
(3)若cn≤![]() m2+m-1对一切正整数n恒成立,求实数m的取值范围.
m2+m-1对一切正整数n恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是棱长为3的正方体,点
是棱长为3的正方体,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() ,(1)求证:
,(1)求证: ![]() 四点共面; (2)若点
四点共面; (2)若点![]() 在
在![]() 上,
上, ![]() ,点
,点![]() 在
在![]() 上,
上, ![]() ,垂足为
,垂足为![]() ,求证:
,求证: ![]() 面
面![]() ; (3)用
; (3)用![]() 表示截面
表示截面![]() 和面
和面![]() 所成锐二面角大小,求
所成锐二面角大小,求![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上. 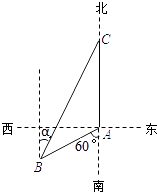
(1)求渔船甲的速度;
(2)求sinα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂最近十年生产总量逐年上升,如表是部分统计数据:
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
生产总量(万吨) |
(Ⅰ)利用所给数据求年生产总量与年份之间的回归直线方程![]() ;
;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该厂2018年生产总量.
(回归直线的方程: ![]() ,其中
,其中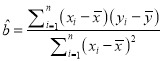 ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com