
����Ŀ���������ҹ��Ĺ��⣬�ǡ����Ҽ��������Ļ��Ų�����ij�����������ϵ��鷢�ָ��ؾ���Ʊ�ѵ�����![]() ������̬�ֲ�
������̬�ֲ�![]() ͬʱ�����ȡ
ͬʱ�����ȡ![]() λ����ij����̨���Ұ����硷��Ŀ��Ʊ�ѵ�������Ϊ�������з����о���ȫ��Ʊ�ѵ����䶼��
λ����ij����̨���Ұ����硷��Ŀ��Ʊ�ѵ�������Ϊ�������з����о���ȫ��Ʊ�ѵ����䶼��![]() �ڣ����������ݷֱ�����Ϊ
�ڣ����������ݷֱ�����Ϊ![]() �ɴ˵õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
�ɴ˵õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.

(��) ��![]() ��
��![]() ��ֵ��
��ֵ��
�����ִ�����������![]() ��Ʊ������֯��һ���йؾ���֪ʶ���ʴ�ÿ�˻ش�һ�����⣬���Ӯ��һ̨����Ϸ���ݳ��������û�н�Ʒ������ÿ�˴�Եĸ��ʾ�Ϊ
��Ʊ������֯��һ���йؾ���֪ʶ���ʴ�ÿ�˻ش�һ�����⣬���Ӯ��һ̨����Ϸ���ݳ��������û�н�Ʒ������ÿ�˴�Եĸ��ʾ�Ϊ![]() ����ÿ���˻ش���ȷ����֮��û��Ӱ�죬��
����ÿ���˻ش���ȷ����֮��û��Ӱ�죬��![]() ��ʾƱ����Ӯ������Ϸ���ݳ�����̨������
��ʾƱ����Ӯ������Ϸ���ݳ�����̨������![]() �ķֲ��м���ѧ����.
�ķֲ��м���ѧ����.

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=2sin����2x+ ![]() ����ͼ������ƽ��
����ͼ������ƽ�� ![]() ����λ�õ���ͼ���Ӧ�Ľ���ʽӦ���ǣ� ��
����λ�õ���ͼ���Ӧ�Ľ���ʽӦ���ǣ� ��
A.y=��2sin��2x��
B.y=��2sin��2x+ ![]() ��
��
C.y=��2sin��2x�� ![]() ��
��
D.y=��2sin��2x+ ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
��1����![]() ��֤��
��֤��![]() ��
��
��2����![]() ����
����![]() ��ȡֵ��Χ����֤����ʱ
��ȡֵ��Χ����֤����ʱ![]() �ļ�ֵ��������
�ļ�ֵ��������![]() ��.
��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=sin����x+�գ����أ�0��|��|�� ![]() ���IJ���ͼ����ͼ��ʾ��
���IJ���ͼ����ͼ��ʾ�� 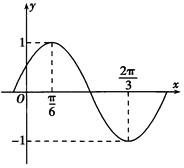
��1������f��x���Ľ���ʽ����д��f��x���ĵ��������䣻
��2����֪��ABC���ڽǷֱ���A��B��C��AΪ��ǣ���f�� ![]() ��
�� ![]() ��=
��= ![]() ����cosA��ֵ��
����cosA��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
�� ![]() ��
�� ![]() ƽ��
ƽ��![]() ��
�� ![]() .
.
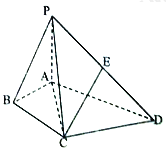
(1)���![]() Ϊ
Ϊ![]() ���е㣬��֤��
���е㣬��֤�� ![]() ƽ��
ƽ��![]() ��
��
(2)�߶�![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ��ֱ��
��ʹ��ֱ��![]() ��ƽ��
��ƽ��![]() ���ɵĽ�
���ɵĽ�![]() ������ֵΪ
������ֵΪ![]() �������ڣ���ȷ����
�������ڣ���ȷ����![]() ��λ�ã��������ڣ���˵������.
��λ�ã��������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�OΪAC��BD�Ľ��㣬ABƽ��PAD����PAD���������Σ�DC//AB��DA��DC��2AB.
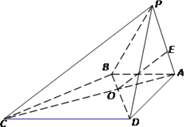
��1������EΪ��PA��һ�㣬��OE��ƽ��PBC����![]() ��ֵ��
��ֵ��
��2����֤��ƽ��PBCƽ��PDC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() Ϊ����ԭ��,��Բ
Ϊ����ԭ��,��Բ![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() �϶���Ϊ
�϶���Ϊ![]() ,�Ҷ���Ϊ
,�Ҷ���Ϊ![]() ,��
,��![]() Ϊֱ����Բ
Ϊֱ����Բ![]() ����
����![]() ,ֱ��
,ֱ��![]() ��Բ
��Բ![]() �ཻ�õ����ҳ�Ϊ
�ཻ�õ����ҳ�Ϊ![]()
��������Բ![]() �ķ��̣�
�ķ��̣�
������ֱ��![]() ����Բ
����Բ![]() �ཻ��
�ཻ��![]() ���㣬
���㣬 ![]() ��
��![]() �ᣬ
�ᣬ ![]() ��ֱ��ཻ��
��ֱ��ཻ��![]() ���㣬���㣺�ټ�
���㣬���㣺�ټ�![]() ���е�Ϊ
���е�Ϊ![]() ,��
,��![]() ���㵽ֱ��
���㵽ֱ��![]() �ľ�����ȣ��ڼ�
�ľ�����ȣ��ڼ�![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() ��
��![]() ȡ�����ֵʱ,��
ȡ�����ֵʱ,��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x��=x2+ax+3��
��1����x��Rʱ��f��x����a���������a��ȡֵ��Χ��
��2����x��[��2��2]ʱ��f��x����a���������a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲC������A����2��0����B��0��2������Բ��C��ֱ��y=x�ϣ���ֱ��l��y=kx+1��ԲC�ཻ��P��Q���㣮
��1����ԲC�ķ��̣�
��2����![]() ����ʵ��k��ֵ��
����ʵ��k��ֵ��
��3�����㣨0��4������ֱ��m��ԲC��E��F���㣮���ʣ�����EFΪֱ��������Բ�У��Ƿ����������ԲP��ʹ��ԲP������M��2��0���������ڣ����ԲP�ķ��̣��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com