
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最小值;
上的最小值;
(2)若![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若![]() ,不等式
,不等式 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3) .
.
【解析】
试题分析:(1)由![]() 时,得出
时,得出![]() ,则
,则![]() ,再求导
,再求导![]() ,可得函数
,可得函数![]() 在
在![]() 上是增函数,从而得到函数
上是增函数,从而得到函数![]() 的单调性,即可求解函数
的单调性,即可求解函数![]() 在
在![]() 上的最小值; (2)由(1)知函数
上的最小值; (2)由(1)知函数![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,使得
,使得![]() ,得
,得![]() ,即
,即![]() ,设
,设![]() ,利用函数
,利用函数![]() 的单调性,即可求解求
的单调性,即可求解求![]() 的取值范围;(3)根据题意,转化为
的取值范围;(3)根据题意,转化为 对任意
对任意![]() 成立,令
成立,令 ,所以
,所以![]() ,可得出
,可得出![]() 的单调性,求解出
的单调性,求解出![]() 的最小值,即可
的最小值,即可![]() 的取值范围.
的取值范围.
试题解析:(1)![]() 时,
时,![]() ,
,![]() ,
,
![]() ,所以函数
,所以函数![]() 在
在![]() 上是增函数,
上是增函数,
又函数![]() 的值域为R,
的值域为R,
故![]() ,使得
,使得![]() ,
,
又![]() ,
,![]() ,所以当
,所以当![]() 时,
时,![]() ,
,
即函数![]() 在区间
在区间![]() 上递增,所以
上递增,所以![]()
(2)![]() ,
,
由(1)知函数![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,使得
,使得![]()
进而函数![]() 在区间
在区间![]() 上递减,在
上递减,在![]() 上递增,
上递增,
由![]() 得:
得:![]() ,
,
![]() ,
,![]() ,
,
因为![]() ,不等式
,不等式![]() 恒成立,
恒成立,
![]()
![]()
(另解:因为![]() ,不等式
,不等式![]() 恒成立,
恒成立,
即![]()
由![]() ,
,
当![]() 时取等号,
时取等号,![]() )
)
(3)由 ,
,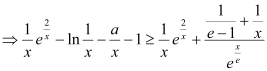 ,
,
 ,
, 对任意
对任意![]() 成立,
成立,
令函数 ,所以
,所以 ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以当![]() 时,函数
时,函数![]() 取得最小值
取得最小值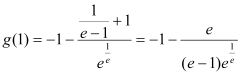 ,
,



科目:高中数学 来源: 题型:
【题目】如图,建立平面直角坐标系![]() ,
,![]() 轴在地平面上,
轴在地平面上,![]() 轴垂直于地平面,单位长度为1千米,某炮位于坐标原点,已知炮弹发射后的轨迹在方程
轴垂直于地平面,单位长度为1千米,某炮位于坐标原点,已知炮弹发射后的轨迹在方程![]() 表示的曲线上,其中
表示的曲线上,其中![]() 与发射方向有关,炮的射程是指炮弹落地点的横坐标.
与发射方向有关,炮的射程是指炮弹落地点的横坐标.

(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标![]() 不超过多少时,炮弹可以击中它?请说明理由.
不超过多少时,炮弹可以击中它?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个四棱锥的三视图如图所示.

(1)求证:PA⊥BD;
(2)在线段PD上是否存在一点Q,使二面角Q-AC-D的平面角为30°?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 由归纳推理得到的结论一定正确
B. 由类比推理得到的结论一定正确
C. 由合情推理得到的结论一定正确
D. 演绎推理在前提和推理形式都正确的前提下,得到的结论一定正确
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若不等式x2-(a+1)x+a≤0的解集是[-4,3]的子集,则a的取值范围是( )
A. [-4,1] B. [-4,3] C. [1,3] D. [-1,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列试验中,是古典概型的为( )
A.种下一粒种子,观察它是否发芽
B.从规格直径为250 mm±0.6 mm的一批合格产品中任意抽一件,测量其直径d
C.抛一枚硬币,观察其向上的面
D.某人射击中靶或不中靶
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用随机数表法进行抽样有以下几个步骤:①将总体中的个体编号;②获取样本号码;③选定开始的数字,这些步骤的先后顺序应为 ( )
A. ①②③ B. ③②①
C. ①③② D. ③①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C上任意一点M满足|MF1|+|MF2|=4,其中F1(![]() ,F2(
,F2(![]() ,
,
(Ⅰ)求曲线C的方程;
(Ⅱ)已知直线![]() 与曲线C交于A,B两点,是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
与曲线C交于A,B两点,是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com