
| 月人均收入x(元) | 300 | 390 | 420 | 504 | 570 | 700 | 760 | 800 | 850 | 1080 |
| 月人均生活费y(元) | 255 | 324 | 330 | 345 | 450 | 520 | 580 | 650 | 700 | 750 |
| ? |
| b |
| |||||||
|
| ? |
| a |
. |
| y |
| ? |
| b |
. |
| x |
. |
| x |
. |
| y |
| ? |
| b |
| |||||||
|
| ? |
| a |
. |
| y |
| ? |
| b |
. |
| x |
| ? |
| y |
| ? |
| y |


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
月人均收入x(元) | 300 | 390 | 420 | 504 | 570 | 700 | 760 | 800 | 850 | 1080 |
月人均生活费y(元) | 255 | 324 | 330 | 345 | 450 | 520 | 580 | 650 | 700 | 750 |
利用上述资料:
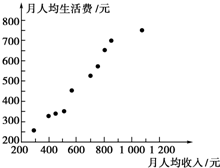
(1)画出散点图;
(2)如果变量x与y之间具有线性相关关系,求出回归直线方程;
(3)测算人均收入为280元时,人均生活费支出应为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
某城区为研究城镇居民月家庭人均生活费支出和月人均收入的相关关系,随机抽取10户进行调查,其结果如下:
月人均收入x(元) | 300 | 390 | 420 | 504 | 570 | 700 | 760 | 800 | 850 | 1 080 |
月人均生活费y(元) | 255 | 324 | 330 | 345 | 450 | 520 | 580 | 650 | 700 | 750 |
利用上述资料:
(1)画出散点图;
(2)如果变量x与y之间具有线性相关关系,求出回归直线方程;
(3)测算人均收入为280元时,人均生活费支出约为多少元?
查看答案和解析>>
科目:高中数学 来源:同步题 题型:解答题

查看答案和解析>>
科目:高中数学 来源:《4.3 相关性、最小二乘估计》2013年高考数学优化训练(文科)(解析版) 题型:解答题
| 月人均收入x(元) | 300 | 390 | 420 | 504 | 570 | 700 | 760 | 800 | 850 | 1080 |
| 月人均生活费y(元) | 255 | 324 | 330 | 345 | 450 | 520 | 580 | 650 | 700 | 750 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com