
已知点(1, 2)在函数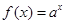 (
(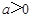 且
且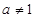 )的图象上,等比数列
)的图象上,等比数列 的前
的前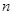 项和为
项和为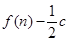 ,数列
,数列
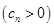 的首项为c,且其前
的首项为c,且其前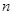 项和
项和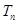 满足 2
满足 2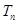 =
=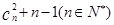 .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列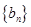 的前
的前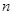 项和
项和 .
.
(1)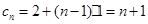
(2)
【解析】(1)因为点(1, 2)是函数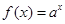 (
(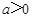 且
且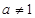 )的图象上,据此可求出
)的图象上,据此可求出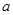 ,因而确定
,因而确定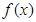 .
.
∵数列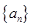 的前
的前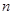 项和为
项和为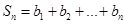 ,所以可得
,所以可得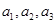 ,根据
,根据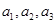 成等比数列,可建立关于c的方程求出c值.进而得到公比q=2.所以
成等比数列,可建立关于c的方程求出c值.进而得到公比q=2.所以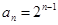 .
.
再根据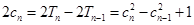 可得到
可得到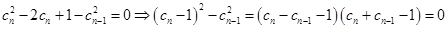 ,
,
因为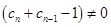 ,可得
,可得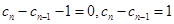 ,进而得到
,进而得到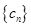 的通项公式.
的通项公式.
∵点(1, 2)是函数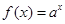 (
(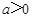 且
且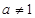 )的图象上,
)的图象上,
∴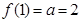 ,∴
,∴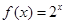 …………………… 1分
…………………… 1分
∵数列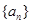 的前
的前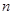 项和为
项和为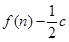 ,∴
,∴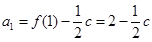 ,
,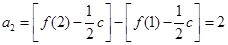 ,
,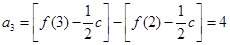
又数列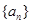 是等比数列,
是等比数列,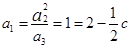 ,∴
,∴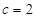 ,公比
,公比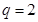 ,……… 4分
,……… 4分
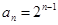 ………………………………5分
………………………………5分
当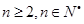 ,
,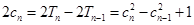 ,
,
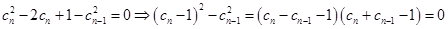 ,
,
∵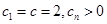 ,∴
,∴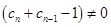 ,∴
,∴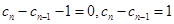 ……… 7分
……… 7分
所以数列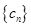 是首项是2,公差是1的等差数列,其通项公式为:
是首项是2,公差是1的等差数列,其通项公式为: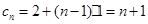
………………………………8分
(2)解本小题的关键是先得到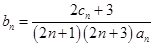
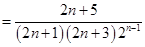 .
.
然后转化成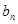
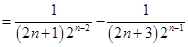 ,再采用裂项求和的方法求和即可.
,再采用裂项求和的方法求和即可.
解:由(1),得
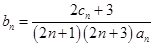
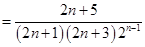 .………………………9分
.………………………9分
所以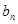
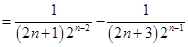 .………11分
.………11分
所以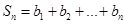
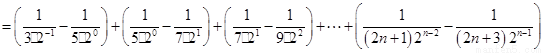 .
.
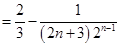 ……………………………13分
……………………………13分
故数列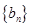 的前
的前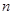 项和
项和 .…………………………14分
.…………………………14分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练23练习卷(解析版) 题型:解答题
在平面直角坐标系xOy中,已知点A(-1,-2),B(2,3),C(-2,-1).
(1)求以线段AB、AC为邻边的平行四边形的两条对角线的长;
(2)设实数t满足( -t
-t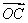 )·
)·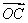 =0,求t的值.
=0,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com