
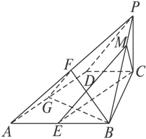
(1)若PB=4PM,求证:CM∥平面PAD;
(2)求证:平面PAB⊥平面PAD;
(3)若点M到平面PAD的距离为![]() ,问点M位于线段PB上哪一位置?
,问点M位于线段PB上哪一位置?
解法1:(1)在AB上取一点E,使得AE=1,则CE∥AD.

又∵AB=4AE,PB=4PM,
∴EM∥PA.
∴平面PAD∥平面MEC.
∴MC∥平面PAD.
(2)分别取PA和AD的中点F、G,连结BF、FG、BG.
∵PB与平面ABC成30°角,
∴∠PBC=30°.
∴PB=4,BP=AB.∴BF⊥AP.
又∵FG=![]() DP=
DP=![]()
![]() ,
,
∵AB⊥面PBC,∴AB⊥PB,BF=![]() .
.
在直角梯形ABCD中,计算得BG=![]() .
.
∵FG2+BF2=BG2,∴BF⊥FG,
∴BF⊥平面PAD.
∴面PAB⊥面PAD.
(3)过点M在平面PAB内作MN∥PA,
∴点M到面PAD的距离即为点N到面PAD的距离,再过点N作NO⊥PA,由面PAB⊥面PAD,
∴NO即为点N到面PAD的距离.
∴NO=![]() =
=![]() .
.
∵NO∥BF,
∴点N为AB的中点.
∴点M为PB的中点.
或直接作MN⊥PA于点N,MN=![]() =
=![]()
又MN∥BF,∴N为PF的中点.
∴点M为PB的中点.
解法2:(1)以C为原点,CD、CB、CP所在直线分别为x、y、z轴建立空间直角坐标系,
∵PC⊥平面ABCD,
∴∠PBC=30°.
∵|PC|=2,
∴|BC|=![]() ,|PB|=4.
,|PB|=4.
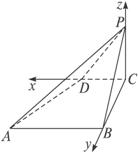
∴D(1,0,0)、B(0,![]() ,0)、A(4,
,0)、A(4,![]() ,0)、P(0,0,2).
,0)、P(0,0,2).
∵PB=4PM,∴M(0,![]() ,
,![]() ),
),
![]() =(0,
=(0,![]() ,
,![]() ),
),
![]() =(-1,0,2),
=(-1,0,2),![]() =(3,
=(3,![]() ,0).
,0).
设![]() =x
=x![]() +y
+y![]() (x、y∈R),
(x、y∈R),
则(0, ![]() ,
,![]() )=x(-1,0,2)+y(3,
)=x(-1,0,2)+y(3, ![]() ,0),
,0),
∴
∴![]() =
=![]()
![]() +
+![]()
![]() .
.
∴![]() 、
、![]() 、
、![]() 共面,
共面,
∵C![]() 平面PAD,
平面PAD,
∴CM∥平面PAD.
(2)作BE⊥PA于E,
∵PB=AB=4,
∴E为PA的中点.
∵E(2,![]() ,1),
,1), ![]() =(2,
=(2,![]() ,1).
,1).
∵![]() ·
·![]() DA=(2,-
DA=(2,-![]() ,1)·(3,
,1)·(3,![]() ,0)=0,
,0)=0,
∴BE⊥DA.又BE⊥PA,
∴BE⊥面PAD.
∴面PAB⊥面PAD.
(3)设![]() =λ
=λ![]() =λ(0,
=λ(0,![]() ,2)=(0,
,2)=(0, ![]() λ,2λ),
λ,2λ),
∵BE⊥面PAD,
∴平面PAD的法向量n=![]() =(2,
=(2,![]() ,1),
,1),
∴点M到平面PAD的距离d=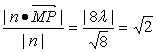 .
.
∴λ=![]() (负的舍去),即点M为线段PB的中点.
(负的舍去),即点M为线段PB的中点.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 (理)设6张卡片上分别写有函数f1(x)=x、f2(x)=x2、f3(x)=x3、f4(x)=sinx、f5(x)=cosx和f6(x)=lg(|x|+1).
(理)设6张卡片上分别写有函数f1(x)=x、f2(x)=x2、f3(x)=x3、f4(x)=sinx、f5(x)=cosx和f6(x)=lg(|x|+1).查看答案和解析>>
科目:高中数学 来源: 题型:044
(2007
湖北部分重点中学模拟)如下图所示,四棱锥P-ABCD中,AB⊥AD,CD⊥AD,PA⊥底面ABCD,PA=AD=CD=2AB=2,M为PC的中点.(1)
求证:BM∥平面PAD;(2)
在侧面PAD内找一点N,使MN⊥平面PBD;(3)
求直线PC与平面PBD所成角的正弦.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com