min{s1,s2,┅,sn},max{s1,s2,┅,sn}分别表示实数s1,s2,┅,sn中的最小者和最大者.
(1)作出函数f(x)=|x+3|+2|x-1|(x∈R)的图象;
(2)在求函数f(x)=|x+3|+2|x-1|(x∈R)的最小值时,有如下结论:f(x)min=min{f(-3),f(1)=4.请说明此结论成立的理由;
(3)仿照(2)中的结论,讨论当a1,a2,┅,an为实数时,函数f(x)=a1|x-x1|+a2|x-x2|+┅+an|x-xn|(x∈R,x1<x2<┅<xn∈R)的最值.
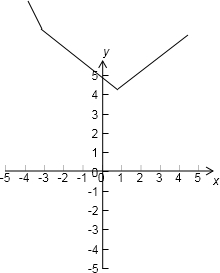
解:(1)f(x)=|x+3|+2|x-1|=
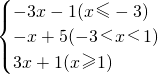
其图象如图
(2)当x∈(-∞,-3)时,f(x)是减函数,
当x∈[-3,1)时,f(x)是减函数,
当x∈[1,+∞)时,f(x)是增函数,
∴f(x)
min=min{f(-3),f(1)}=4.
(3)当a
1+a
2+┅+a
n<0时,f(x)
max=maxf(x
1),f(x
2),┅,f(x
n)};
当a
1+a
2+┅+a
n>0时,f(x)
min=min{f(x
1),f(x
2),┅,f(x
n)};
当a
1+a
2+┅+a
n=0时,f(x)
min=min{f(x
1),f(x
2)},
f(x)
max=maxf(x
1),f(x
n)}.
分析:(1)利用绝对值的意义,对x分段讨论取得绝对值符号,转化为分段函数,分段画出函数的图象.
(2)结合图象得到函数的单调性,利用单调性说明函数的最值在何处取得.
(3)利用类比推理得到一般情况下最值在何处取得.
点评:本题考查利用绝对值的意义分段讨论去绝对值转化为分段函数、利用函数的单调性求函数的最值、类比推理的推理方法.

 解:(1)f(x)=|x+3|+2|x-1|=
解:(1)f(x)=|x+3|+2|x-1|=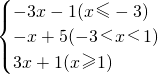 其图象如图
其图象如图

 53随堂测系列答案
53随堂测系列答案