练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20. 已知函数y=kx与y=x2+2（x≥0）的图象相交于不同两点A（x1，y1），B（x2，y2）.l1，l2分别是y=x2+2（x≥0）的图象在A，B两点的切线，M，N分别是l1，l2与x轴的交点.

    （Ⅰ）求k的取值范围；

    （Ⅱ）设t为点M的横坐标，当x1＜x2时，写出t以x1为自变量的函数式，并求其定义域和值域；

    （Ⅲ）试比较|OM|与|ON|的大小，并说明理由（O是坐标原点）.

    解：（Ⅰ）由方程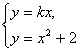消y得x2-kx+2=0，                 ①

    依题意，该方程有两个正实根，

    故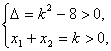解得k＞2.

    （Ⅱ）由f′（x）=2x，求得切线l1的方程为y=2x1（x-x1）+y1.

    由y1=+2，并令y=0，得t=.

    x1，x2是方程①的两实根，且x1＜x2，故x1=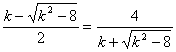，k＞2，

    x1是关于k的减函数，所以x1的取值范围是（0，）.

    t是关于x1的增函数，定义域为（0，），所以值域为（-∞，0）.

    （Ⅲ）当x1＜x2时，由（Ⅱ）可知

    | OM |=| t |= -，

    类似可得| ON |=，

    | OM | - | ON |= -.

    由①可知   x1x2=2，

    从而| OM | - | ON |=0.

    当x2＜x1时，有相同的结果| OM | - | ON |=0.

    所以| OM | = | ON |.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数y=kx与y=log
    1
    2
    x图象的交点横坐标为2，则k的值为（　　）
    A、-
    1
    4
    B、
    1
    4
    C、
    1
    2
    D、-
    1
    2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数y=kx与y=x2+2（x≥0）的图象相交于A（x1，y1），B（x2，y2），l1，l2分别是y=x2+2（x≥0）的图象在A，B两点的切线，M，N分别是l1，l2与x轴的交点．
    （I）求k的取值范围；
    （II）设t为点M的横坐标，当x1＜x2时，写出t以x1为自变量的函数式，并求其定义域和值域；
    （III）试比较|OM|与|ON|的大小，并说明理由（O是坐标原点）．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知函数y=kx与y=log
    1
    2
    x图象的交点横坐标为2，则k的值为（　　）
    A．-
    1
    4
    		B．
    1
    4
    		C．
    1
    2
    		D．-
    1
    2

    查看答案和解析>>

    科目：高中数学 来源：北京高考真题 题型：解答题

    已知函数y=kx与y=x2+2（x≥0）的图象相交于A（x1，y1），B（x2，y2），l1，l2分别是y=x2+2（x≥0）的图象在A，B两点的切线，M，N分别是l1，l2与x轴的交点。
    （1）求k的取值范围；
    （2）设t为点M的横坐标，当x1＜x2时，写出t以x1为自变量的函数式，并求其定义域和值域；
    （3）试比较|OM|与|ON|的大小，并说明理由（O是坐标原点）。

    查看答案和解析>>

    科目：高中数学 来源：2012年江苏省常州中学高考冲刺复习单元卷：函数2（解析版） 题型：解答题

    已知函数y=kx与y=x2+2（x≥0）的图象相交于A（x1，y1），B（x2，y2），l1，l2分别是y=x2+2（x≥0）的图象在A，B两点的切线，M，N分别是l1，l2与x轴的交点．
    （I）求k的取值范围；
    （II）设t为点M的横坐标，当x1＜x2时，写出t以x1为自变量的函数式，并求其定义域和值域；
    （III）试比较|OM|与|ON|的大小，并说明理由（O是坐标原点）．

    查看答案和解析>>

    同步练习册答案