
【题目】已知函数 ![]()
(1)求函数f(x)在 ![]() 上的最大值与最小值;
上的最大值与最小值;
(2)已知 ![]() ,x0∈(
,x0∈( ![]() ,
, ![]() ),求cos4x0的值.
),求cos4x0的值.
【答案】
(1)解:函数 ![]()
化简可得:3 ![]() +
+ ![]() sin2x﹣
sin2x﹣ ![]()
= ![]() ﹣
﹣ ![]() cos2x×
cos2x× ![]() +
+ ![]() ×
× ![]() sin2x+
sin2x+ ![]() sin2x﹣
sin2x﹣ ![]() ﹣
﹣ ![]() cos2x
cos2x
= ![]() sin2x﹣cos2x+
sin2x﹣cos2x+ ![]()
=2sin(2x﹣ ![]() )+
)+ ![]() .
.
∵x∈ ![]() 上,
上,
∴2x﹣ ![]() ∈[
∈[ ![]() ,
, ![]() ].
].
∴sin(2x﹣ ![]() )∈[
)∈[ ![]() ,1].
,1].
函数f(x)在 ![]() 上的最大值为
上的最大值为 ![]() ,最小值为
,最小值为 ![]() .
.
(2)解:∵ ![]() ,即2sin(4x0﹣
,即2sin(4x0﹣ ![]() )+
)+ ![]() =
= ![]()
sin(4x0﹣ ![]() )=
)= ![]()
∵x0∈( ![]() ,
, ![]() ),
),
4x0﹣ ![]() ∈[
∈[ ![]() ,π],
,π],
∴cos(4x0﹣ ![]() )=
)= ![]() .
.
cos4x0=cos[4x0﹣ ![]() )
) ![]() ]=cos(4x0﹣
]=cos(4x0﹣ ![]() )cos
)cos ![]() ﹣sin(4x0﹣
﹣sin(4x0﹣ ![]() )sin
)sin ![]() =
= ![]() ×
× ![]() ﹣
﹣ ![]() =
= ![]() .
.
【解析】(1)根据二倍角和两角差的正弦公式将f(x)化简为f(x)=Asin(ωx+φ)的形式,结合正弦函数的图象和性质可得到在给定区间的最值,(2)由题意代入找得到sin(4x0﹣ ![]() ),cos(4x0﹣
),cos(4x0﹣ ![]() )的值,根据cos4x0=cos[(4x0﹣
)的值,根据cos4x0=cos[(4x0﹣ ![]() ) +
) + ![]() ],由两角和的余弦公式展开代值可求得.
],由两角和的余弦公式展开代值可求得.


科目:高中数学 来源: 题型:
【题目】如图所示,抛物线C:x2=2py(p>0),其焦点为F,C上的一点M(4,m)满足|MF|=4.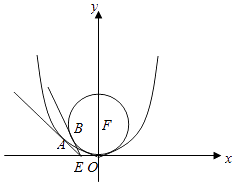
(1)求抛物线C的标准方程;
(2)过点E(﹣1,0)作不经过原点的两条直线EA,EB分别与抛物线C和圆F:x2+(y﹣2)2=4相切于点A,B,试判断直线AB是否经过焦点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域[﹣1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示
x | ﹣1 | 0 | 2 | 4 | 5 |
F(x) | 1 | 2 | 1.5 | 2 | 1 |
下列关于函数f(x)的命题;
①函数f(x)的值域为[1,2];
②函数f(x)在[0,2]上是减函数
③如果当x∈[﹣1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)﹣a最多有4个零点.
其中正确命题的序号是 . 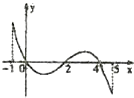
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(n)=1+ ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ,g(n)=
,g(n)= ![]() ﹣
﹣ ![]() ,n∈N* .
,n∈N* .
(1)当n=1,2,3时,试比较f(n)与g(n)的大小关系;
(2)猜想f(n)与g(n)的大小关系,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为 ![]() (a为常数,n∈N*).
(a为常数,n∈N*).
(1)求a1 , a2 , a3;
(2)若数列{an}为等比数列,求常数a的值及an .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有4个新毕业的老师要分配到四所学校任教,每个老师都有分配(结果用数字表示).
(1)共有多少种不同的分配方案?
(2)恰有一个学校不分配老师,有多少种不同的分配方案?
(3)某个学校分配了2个老师,有多少种不同的分配方案?
(4)恰有两个学校不分配老师,有多少种不同的分配方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 有两个极值点x1 , x2 , 且x1<x2 , 记点M(x1 , f(x1)),N(x2 , f(x2)).
有两个极值点x1 , x2 , 且x1<x2 , 记点M(x1 , f(x1)),N(x2 , f(x2)).
(Ⅰ)求直线MN的方程;
(Ⅱ)证明:线段MN与曲线y=f(x)有且只有一个异于M、N的公共点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com