
【题目】如图所示,抛物线C:x2=2py(p>0),其焦点为F,C上的一点M(4,m)满足|MF|=4.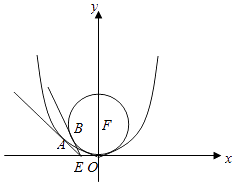
(1)求抛物线C的标准方程;
(2)过点E(﹣1,0)作不经过原点的两条直线EA,EB分别与抛物线C和圆F:x2+(y﹣2)2=4相切于点A,B,试判断直线AB是否经过焦点F.
【答案】
(1)解:抛物线C的准线方程为 ![]() ,
,
∴|MF|=m+ ![]() =4,
=4,
由M(4,m)在椭圆上,
∴16=2pm,
∴p2﹣8p+16=0,解得p=4,
∴抛物线C的标准方程为x2=8y
(2)解:设EA:x=ky﹣1,联立 ![]() ,消去x得:k2y2﹣(2k+8)y+1=0,
,消去x得:k2y2﹣(2k+8)y+1=0,
∵EA与C相切,
∴△=(2k+8)2﹣4k2=0,解得k=﹣2,
∴ ![]() ,求得
,求得 ![]() ,
,
设EB:x=ty﹣1,联立 ![]() ,消去x得:(t2+1)y2﹣(2t+4)y+1=0,
,消去x得:(t2+1)y2﹣(2t+4)y+1=0,
∵EB与圆F相切,
∴△=(2t+4)2﹣4(t2+1)=0,即 ![]() ,
,
∴ ![]() ,求得
,求得 ![]() ,
,
∴直线AB的斜率 ![]() ,
,
可得直线AB的方程为 ![]() ,经过焦点F(0,2)
,经过焦点F(0,2)
【解析】1、利用抛物线的定义可得m+ ![]() =4,点M(4,m)在椭圆上,所以16=2pm,即可求出p=4,进而得到抛物线C的标准方程为x2=8y。
=4,点M(4,m)在椭圆上,所以16=2pm,即可求出p=4,进而得到抛物线C的标准方程为x2=8y。
2、首先联立直线与抛物线的方程,根据题意令△=0,求得k=﹣2,即得点A的坐标;同理可得点B的坐标,进而得到直线AB的斜率 k AB的值,从而求出直线的方程,并可判断其经过焦点F(0,2)。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆Γ: ![]() =1(a>b>0)的右焦点为(2
=1(a>b>0)的右焦点为(2 ![]() ,0),且椭圆Γ上一点M到其两焦点F1 , F2的距离之和为4
,0),且椭圆Γ上一点M到其两焦点F1 , F2的距离之和为4 ![]() .
.
(Ⅰ)求椭圆Γ的标准方程;
(Ⅱ)设直线l:y=x+m(m∈R)与椭圆Γ交于不同两点A,B,且|AB|=3 ![]() .若点P(x0 , 2)满足|
.若点P(x0 , 2)满足| ![]() |=|
|=| ![]() |,求x0的值.
|,求x0的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,且△ABC为等边三角形,AA1=AB=6,D为AC的中点.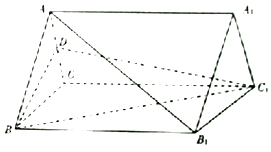
(1)求证:直线AB1∥平面BC1D;
(2)求证:平面BC1D⊥平面ACC1A1;
(3)求三棱锥C﹣BC1D的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.一条直线与一个平面平行,它就和这个平面内的任意一条直线平行
B.平行于同一个平面的两条直线平行
C.与两个相交平面的交线平行的直线,必平行于这两个平面
D.平面外两条平行直线中的一条与这个平面平行,则另一条也与这个平面平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知正方体ABCD-A1B1C1D1.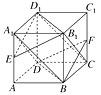
(1)求证:平面A1BD∥平面B1D1C.
(2)若E , F分别是AA1 , CC1的中点,求证:平面EB1D1∥平面FBD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于棱锥、棱台的说法,其中不正确的是( )
A.棱台的侧面一定不会是平行四边形
B.棱锥的侧面只能是三角形
C.由四个面围成的封闭图形只能是三棱锥
D.棱锥被平面截成的两部分不可能都是棱锥
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com