
【题目】若不等式ax2﹣bx+c>0的解集为{x|﹣2<x<3},求不等式cx2﹣bx﹣a<0的解集.
【答案】解:根据题意,若不等式ax2﹣bx+c>0的解集为{x|﹣2<x<3},
则﹣2,3是对应方程ax2+bx+c=0的两个根,且a<0,
则有 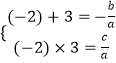 ,解可得b=﹣a,c=﹣6a,
,解可得b=﹣a,c=﹣6a,
则不等式cx2+bx+a>0等价为﹣6ax2﹣ax+a>0,
又由a<0,
则有6x2+x﹣1>0,
即(2x+1)(3x﹣1)>0,
解可得x> ![]() 或x<﹣
或x<﹣ ![]() ,
,
故不等式cx2﹣bx﹣a<0的解集为{x|x> ![]() 或x<﹣
或x<﹣ ![]() }.
}.
【解析】根据不等式的解集与一元二次方程根的情况,利用韦达定理可求出b=﹣a,c=﹣6a,得到新的不等式,因为a<0所以得到6x2+x﹣1>0,解得即可。
【考点精析】解答此题的关键在于理解解一元二次不等式的相关知识,掌握求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】二次函数f(x),又 ![]() 的图象与x轴有且仅有一个公共点,且f′(x)=1﹣2x.
的图象与x轴有且仅有一个公共点,且f′(x)=1﹣2x.
(1)求f(x)的表达式.
(2)若直线y=kx把y=f(x)的图象与x轴所围成的图形的面积二等分,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +lnx,其中a为常数,e为自然对数的底数.
+lnx,其中a为常数,e为自然对数的底数.
(I)若a=1,求函数f(x)的单调区间;
(II)若函数f(x)在区间[1,2]上为单调函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知( ![]() +x2)2n的展开式中各项系数的和比(3x﹣1)n的展开式中二项式系数的和大992,求(2x﹣
+x2)2n的展开式中各项系数的和比(3x﹣1)n的展开式中二项式系数的和大992,求(2x﹣ ![]() )2n的展开式中:
)2n的展开式中:
(1)第10项
(2)常数项;
(3)系数的绝对值最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、N分别是BD和AE的中点,那么①AD⊥MN;②MN∥平面CDE;③MN∥CE;④MN、CE异面.其中假命题的个数为( )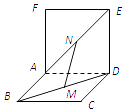
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l经过点M(﹣3,﹣3),且圆x2+y2+4y﹣21=0的圆心到l的距离为 ![]() .
.
(1)求直线l被该圆所截得的弦长;
(2)求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x3﹣ax在(﹣∞,﹣1]上是单调函数,则a的取值范围是( )
A.(3,+∞)
B.[3,+∞)
C.(﹣∞,3)
D.(﹣∞,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,抛物线C:x2=2py(p>0),其焦点为F,C上的一点M(4,m)满足|MF|=4.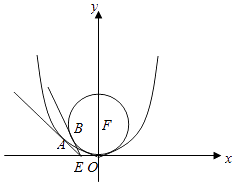
(1)求抛物线C的标准方程;
(2)过点E(﹣1,0)作不经过原点的两条直线EA,EB分别与抛物线C和圆F:x2+(y﹣2)2=4相切于点A,B,试判断直线AB是否经过焦点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域[﹣1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示
x | ﹣1 | 0 | 2 | 4 | 5 |
F(x) | 1 | 2 | 1.5 | 2 | 1 |
下列关于函数f(x)的命题;
①函数f(x)的值域为[1,2];
②函数f(x)在[0,2]上是减函数
③如果当x∈[﹣1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)﹣a最多有4个零点.
其中正确命题的序号是 . 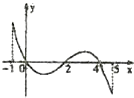
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com