练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    求函数的定义域、值域和单调区间.

    解析:注意到对数函数的图象及性质和复合函数的单调性.

    答案:由μ(x)=x2-5x+4＞0,解得x＞4或x＜1,?

    所以x∈(-∞,1)∪(4,+∞).?

    当x∈(-∞,1)∪(4,+∞)时,{μ|μ=x2-5x+4}=R +,

    所以函数的值域是R +.

    因为函数是由与μ(x)=x2-5x+4复合而成,函数在其定义域上是单调递减的,函数μ(x)=x 2-5x+4在(-∞,)上为减函数,在［,+∞)上为增函数.考虑到函数的定义域及复合函数单调性,的增区间是定义域内使为减函数、μ(x)=x 2-5x+4也为减函数的区间,即(-∞,1); 的减区间是定义域内使为减函数、μ(x)=x 2-5x+4为增函数的区间,即(4,+∞).


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f（x）=loga（a-ax）且a＞1，
    （1）求函数的定义域和值域；
    （2）讨论f（x）在其定义域上的单调性；
    （3）证明函数图象关于y=x对称．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数y=loga（1-ax）  （a＞0且a≠1）
    （1）求函数的定义域和值域；
    （2）证明函数的图象关于直线y=x对称．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

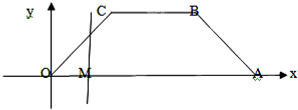    如图，等腰梯形OABC，底角为45°，各顶点的坐标分别为O（0，0），A（6，0），B（4，2），C（2，2）．一条与y轴平行的动直线l从O点开始做平行移动，到A点为止．设直线l与x轴的交点M，记OM=x，记梯形被直线l截得的在l左侧的图形面积为y．
    （1）函数y=f（x）的解析式；
    （2）求函数的定义域、值域；
    （3）计算[f（
    72
    ）]的值．

    查看答案和解析>>

    科目：高中数学 来源：2012年苏教版高中数学必修1 2.4幂函数练习卷（解析版） 题型：解答题

    （本题满分16分）已知幂函数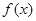的图象经过点.

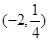    (Ⅰ) 求函数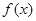的定义域和值域；          (Ⅱ) 证明：函数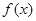在（0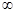，+）上是减函数.

     

    查看答案和解析>>

    科目：高中数学 来源：2012年人教B版高中数学必修一3.2对数函数练习卷（二）（解析版） 题型：解答题

    已知函数f(x)=loga(a－ax)且a＞1，

    （1）求函数的定义域和值域；

    （2）讨论f(x)在其定义域上的单调性；

    （3）证明函数图象关于y=x对称．

     

    查看答案和解析>>

    同步练习册答案