
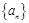 中,
中,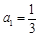 ,且前
,且前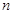 项的算术平均数等于第
项的算术平均数等于第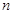 项的
项的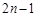 倍(
倍(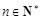 ). (即
). (即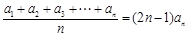
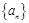 的通项公式,并加以证明.
的通项公式,并加以证明.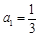 ,
,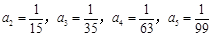 ;
;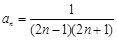 ,证明见解析
,证明见解析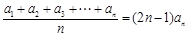 的本质是
的本质是 ,然后令n=1,2,3,4,5,求出前5项即可。
,然后令n=1,2,3,4,5,求出前5项即可。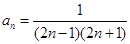 ,由于要证明的结论与n有关,可以考虑采用数学归纳法进行证明:证明要分两个步骤进行:(i)说明n=1时命题成立。(2)先假设n=k时,命题成立;再证明n=k+1时,命题也成立,在证明时要用上n=k时的归纳假设。
,由于要证明的结论与n有关,可以考虑采用数学归纳法进行证明:证明要分两个步骤进行:(i)说明n=1时命题成立。(2)先假设n=k时,命题成立;再证明n=k+1时,命题也成立,在证明时要用上n=k时的归纳假设。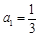 ,
,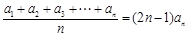 ,分别取
,分别取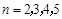 ,
,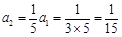 ,
,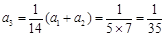 ,
, ,
,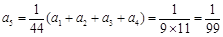 ,所以数列的前5项是:
,所以数列的前5项是: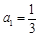 ,
,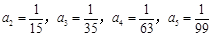 .__4分
.__4分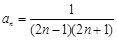 .______6分
.______6分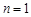 时,公式显然成立.②假设当
时,公式显然成立.②假设当 时成立,即
时成立,即 ,那么由已知,
,那么由已知,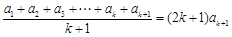 ,
,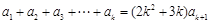 ,所以
,所以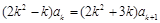 ,
, ,又由归纳假设,得
,又由归纳假设,得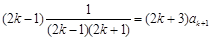 ,
,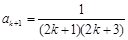 ,即当
,即当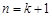 时,公式也成立.
时,公式也成立.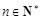 ,都有
,都有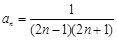 成立. ----------14分
成立. ----------14分

科目:高中数学 来源:不详 题型:单选题
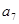 等于()
等于()| A. 22 | B. 21 | C. 19 | D. 18 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
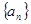 的前三项与数列
的前三项与数列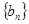 的前三项对应相同,且
的前三项对应相同,且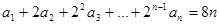 对任意的
对任意的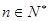 都成立,数列
都成立,数列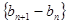 是等差数列
是等差数列
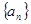 与
与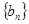 的通项公式;
的通项公式;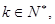 使得
使得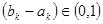 ?请说明理由。
?请说明理由。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com