练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数图象的一部分如图所示．

    （1）求函数的解析式；

    （2）当时，求函数的最大值与最小值及相应的的值．


    解　(1)由图象知A＝2，T＝8，∵T＝＝8，∴ω＝.

    又图象过点(－1,0)，∴2sin＝0.∵|φ|<，∴φ＝.∴f(x)＝2sin.（6分）

    (2)y＝f(x)＋f(x＋2)＝2sin＋2sin＝2sin＝2cos x.

    ∵x∈，∴－≤x≤－.

    ∴当x＝－，即x＝－时，y＝f(x)＋f(x＋2)取得最大值；

    当x＝－π，即x＝－4时，y＝f(x)＋f(x＋2)取得最小值－2.（12分）


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知样本的平均数是，标准差是，则      

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若一个圆锥的底面圆的半径为3，母线长为5，其内有一个内接圆柱（下底面在圆锥的底面上，上底面的圆在圆锥的侧面上），则当这个圆柱的侧面积最大时，其高为　　　（　　）

    A．1        B．2        C．3        D．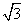

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知中，分别为的对边，，则为（  ）

    A．等腰三角形  B．直角三角形   C．等腰直角三角形   D．等腰或直角三角形

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知，sin()=－ sin则cos=    _．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数 的最小正周期为，则该函数的图象（   ）

    A．关于点对称             B．关于直线对称

    C．关于点对称          D．关于直线对称

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某人要作一个三角形，要求它的三条高的长度分别是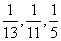，则此人将（   ） 

    A.不能作出满足要求的三角形；    B.作出一个锐角三角形；

    C.作出一个直角三角形；          D.作出一个钝角三角形。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知，则的值为

    A．                          B．                        C．                      D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为“同族函数”，则函数解析式为y＝x2＋1，值域为{1,3}的同族函数有(　　)

    A．1个       B．2个       C．3个      D．4个

    查看答案和解析>>

    同步练习册答案