Question

【题目】在正三棱柱ABC﹣A1B1C1中，若AB1⊥BC1 ， 则下列关于直线A1C和AB1 ， BC1的关系的判断正确的为（ ）
A.A1C和AB1 ， BC1都垂直
B.A1C和AB1垂直，和BC1不垂直
C.A1C和AB1 ， BC1都不垂直
D.A1C和AB1不垂直，和BC1垂直

Answer 1

【答案】A
【解析】解：设D为BC的中点，连结AD、B1D，设E为AB的中点，连结CE、A1E， ∵△ABC是正三角形，∴AD⊥BC，
由正三棱柱的性质可知，平面ABC⊥平面BB1C1C，
又平面ABC∩平面BB1C1C=BC，∴AD⊥平面BB1C1C，
∴B1D是AB1在平面BB1C1C上的射影，
同理，A1E是A1C在平面AA1B1B上的射影，
∵AB1⊥BC1 ， 由三垂线逆定理可知，B1D⊥BC1 ，
∵长方形AA1B1B≌长方形BB1C1 ， ∴A1E⊥AB1 ， 由三垂线定理可知，AB1⊥A1C；
取AC中点F，连结BF、C1F，
∵△ABC是等边三角形，∴BF⊥AC，∵AA1⊥平面ABC，∴BF⊥AA1 ，
∵AA1∩AC=A，∴BF⊥平面ACC1A1 ， ∵A1C平面ACC1A1 ， ∴BF⊥A1C，
∵长方形AA1B1B≌长方形BB1C1≌长方形AA1C1C，∴A1C⊥C1F，由三垂线定理可知，BC1⊥A1C．
∴A1C和AB1 ， BC1都垂直．
故选：A．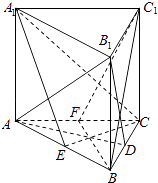

【考点精析】通过灵活运用空间中直线与平面之间的位置关系，掌握直线在平面内—有无数个公共点；直线与平面相交—有且只有一个公共点；直线在平面平行—没有公共点即可以解答此题．