
(本题12分)已知函数 .
.
(1)当 时,求函数
时,求函数 的单调递减区间;
的单调递减区间;
(2)当 时,
时, 在
在 上恒大于0,求实数
上恒大于0,求实数 的取值范围.
的取值范围.
(1) 
(2) 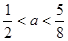
【解析】解:(1) ,
,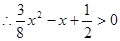 ,得
,得 ,
,
函数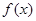 在区间
在区间 上递减. ……………………………………………4分
上递减. ……………………………………………4分
(2)由题意得, 对任意的
对任意的 恒成立 ………………1分
恒成立 ………………1分
法一: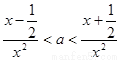 ,对任意的
,对任意的 恒成立
恒成立
所以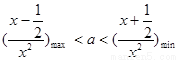 ,
, ………………………………2分
………………………………2分
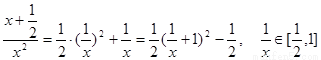 ,所以
,所以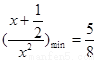 …2分
…2分
同理 …………………………………………………………2分
…………………………………………………………2分
所以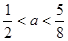 ………………………………………………………………1分
………………………………………………………………1分
法二: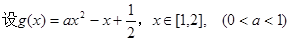
 ………………………………………………1分
………………………………………………1分
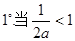 ,即
,即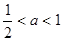 时,
时,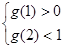 ,解得
,解得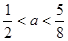 .
.
 ,即
,即 时,
时, ,无解.
,无解.
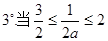 ,即
,即 时,
时, ,无解.
,无解.
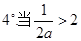 ,即
,即 时,
时, ,无解. ……………………6分
,无解. ……………………6分
综上: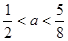 . …………………………………………………………1分
. …………………………………………………………1分
法三:由题意得, 对任意的
对任意的 恒成立 ……………1分
恒成立 ……………1分
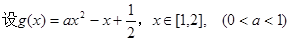 ,
,
则 ,解得
,解得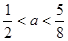 . ………………………………………3分
. ………………………………………3分
再验证:当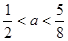 时,
时,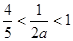 ,
,
所以, ,
, ,
,
故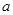 的取值范围为
的取值范围为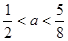 . …………………………………………………4分
. …………………………………………………4分


 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源:2012-2013学年福建省福州外国语学校高三上学期期中考试理科数学试卷(解析版) 题型:解答题
(本题12分)
已知函 有极值,且曲线
有极值,且曲线 处的切线斜率为3.
处的切线斜率为3.
(1)求函数 的解析式;
的解析式;
(2)求 在[-4,1]上的最大值和最小值。
在[-4,1]上的最大值和最小值。
(3)函数 有三个零点,求实数
有三个零点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com