
(本题12分)
已知函 有极值,且曲线
有极值,且曲线 处的切线斜率为3.
处的切线斜率为3.
(1)求函数 的解析式;
的解析式;
(2)求 在[-4,1]上的最大值和最小值。
在[-4,1]上的最大值和最小值。
(3)函数 有三个零点,求实数
有三个零点,求实数 的取值范围.
的取值范围.
(1)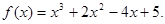
(2)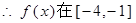 上的最大值为13,最小值为-11。
上的最大值为13,最小值为-11。
(3)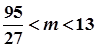 。
。
【解析】
试题分析:(1)利用导数的几何意义得到参数a,b的值。
(2)求解导数判定函数的单调性,进而得到极值,和端点值,比较大小得到最值。
(3)根据函数单调性,确定极大值和极小值的符号,使得有三个零点。
解:(1)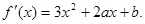 ……………………1分
……………………1分
由题意,得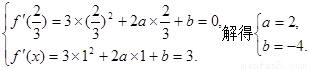 …………3分
…………3分
所以,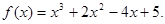 …………………………4分
…………………………4分
(2)由(1)知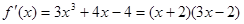
令 ……………………5分
……………………5分
|
x |
-4 |
(-4, -2) |
-2 |
(-2, |
|
( |
1 |
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
|
↗ |
极大值 |
↘ |
极小值 |
↗ |
|
|
函数值 |
--11 |
|
13 |
|
|
|
4 |
…………………………………………………………………………8分
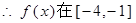 上的最大值为13,最小值为-11。………9分
上的最大值为13,最小值为-11。………9分
(3)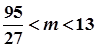 ……………………………………12分
……………………………………12分
考点:本试题主要考查了导数在研究函数中的运用。
点评:解决该试题的关键利用导数的符号判定函数的单调性进而确定其最值。


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源:2012-2013学年福建省高三第一次月考理科数学试卷(解析版) 题型:解答题
(本题12分)已知函数 的图像关于原点对称,并且当
的图像关于原点对称,并且当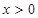 时,
时, ,试求
,试求 在
在 上的表达式,并画出它的图像,根据图像写出它的单调区间。
上的表达式,并画出它的图像,根据图像写出它的单调区间。
查看答案和解析>>
科目:高中数学 来源:2010年浙江省杭州市七校高一上学期期中考试数学试卷 题型:解答题
(本题12分)已知函数 .
.
(1)当 时,求函数
时,求函数 的单调递减区间;
的单调递减区间;
(2)当 时,
时, 在
在 上恒大于0,求实数
上恒大于0,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:陕西省2009-2010学年度第二学期期末考试高二数学(文科)试题 题型:解答题
(本题12分)已知关于 的不等式
的不等式 ,其中
,其中 .
.
(Ⅰ)当 变化时,试求不等式的解集
变化时,试求不等式的解集 ;
;
(Ⅱ)对于不等式的解集 ,若满足
,若满足 (其中
(其中 为整数集). 试探究集合
为整数集). 试探究集合 能否为有限集?若能,求出使得集合
能否为有限集?若能,求出使得集合 中元素个数最少的
中元素个数最少的 的所有取值,并用列举法表示集合
的所有取值,并用列举法表示集合 ;若不能,请说明理由.
;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com