
分析 (1)若f(x)是R上的偶函数,则f(-x)=f(x)恒成立,即3-x+a•3x=3x+a•3-x恒成立,解得a值;
(2)通过a=0,化简函数的表达式,可得函数的图象,数形结合可得方程g(x)-m=0有两解时m的取值范围;
(3)利用a<0,判断函数f(x)在定义域内的单调增函数,利用函数的单调性的定义直接证明即可.
解答 解:(1)∵f(x)是R上的偶函数,
∴f(-x)=f(x)恒成立,
∴3-x+a•3x=3x+a•3-x恒成立,
∴(a-1)(3x-3-x)=0恒成立,
∴a-1=0,
解得:a=1;
(2)若a=0,则函数g(x)=$\left\{\begin{array}{l}{3}^{x}+1(x<0)\\-x+2(x≥0)\end{array}\right.$,其图象如下图所示: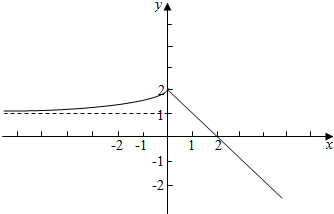
若方程g(x)-m=0有两解,则函数g(x)的图象与直线y=m有两个交点,
由图可得:m∈(1,2);
(3)若a<0,则函数f(x)在定义域R内的单调增减,理由如下:
任取任取x1,x2∈R,且x1<x2,
则0<3x1<3x2,
∴3x1-3x2<0,1-$\frac{a}{{3}^{{x}_{1}}•{3}^{{x}_{2}}}$>0,
f(x1)-f(x2)=(3x1+a•3-x1)-(3x2+a•3-x2)=(3x1-3x2)+a($\frac{{3}^{{x}_{2}}-{3}^{{x}_{1}}}{{3}^{{x}_{1}}•{3}^{{x}_{2}}}$)=(3x1-3x2)(1-$\frac{a}{{3}^{{x}_{1}}•{3}^{{x}_{2}}}$)<0,
∴f(x1)-f(x2)<0,
∴f(x1)<f(x2),
函数f(x)在定义域内的是增函数.
点评 本题考查的知识点是函数的奇偶性,函数的单调性,数形结合思想,方程的根与函数零点的关系,难度中档.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$-1 | B. | 2$\sqrt{6}$ | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4032 | B. | 4030 | C. | 2016 | D. | 2015 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
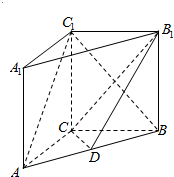 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=3,BC=4,AA1=4,点D是AB的中点,
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=3,BC=4,AA1=4,点D是AB的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com