
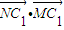 的取值范围.
的取值范围.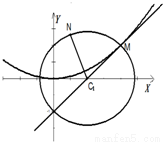
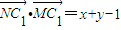 ,再令x+y-1=t,代入圆的方程,然后利用方程有根即△≥0得到答案.
,再令x+y-1=t,代入圆的方程,然后利用方程有根即△≥0得到答案.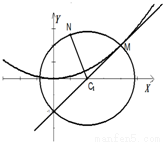 解:(Ⅰ)由题意可得:把M(2,1)代入C2:x2=2py(p>0),
解:(Ⅰ)由题意可得:把M(2,1)代入C2:x2=2py(p>0),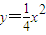 得
得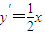 ,
, ,
, ,
, ,(8分)
,(8分)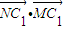 的取值范围为[-2,2].(12分)
的取值范围为[-2,2].(12分)

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
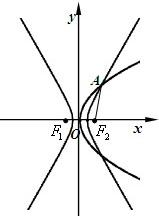 如图,抛物线C1:y2=8x与双曲线C2:
如图,抛物线C1:y2=8x与双曲线C2:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
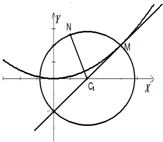 如图,圆C1:(x-a)2+y2=r2(r>0)与抛物线C2:x2=2py(p>0)的一个交点M(2,1),且抛物线在点M处的切线过圆心C1.
如图,圆C1:(x-a)2+y2=r2(r>0)与抛物线C2:x2=2py(p>0)的一个交点M(2,1),且抛物线在点M处的切线过圆心C1.| NC1 |
| MC1 |
查看答案和解析>>
科目:高中数学 来源:福建省师大附中2012届高三高考模拟数学文科试题 题型:044
如图,圆C1:(x-a)2+y2=r2(r>0)与抛物线C2:x2=2py(p>0)的一个交点M(2,1),且抛物线在点M处的切线过圆心C1.
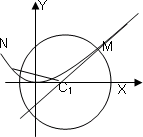
(Ⅰ)求C1和C2的标准方程;
(Ⅱ)若点N为抛物线C2上的一动点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:云南省月考题 题型:解答题
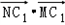 的取值范围.
的取值范围.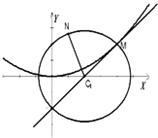
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com