Question

20．设F₁、F₂为椭圆$\frac{{x}^{2}}{4}$+y²=1的两个焦点，P为椭圆上的一点．当△F₁PF₂的面积为1，$\overrightarrow{{PF}_{1}}$•$\overrightarrow{{PF}_{2}}$的值为0．

Answer 1

分析 作图，从而可得a=2，b=1，c=$\sqrt{3}$，不妨设P（x，y）（x＞0，y＞0）；从而可得y=$\frac{\sqrt{3}}{3}$，x=$\frac{2\sqrt{6}}{3}$；从而求数量积即可．

解答 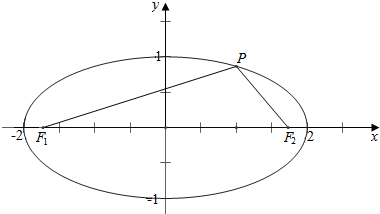解：作图如右图，
由题意得，a=2，b=1，c=$\sqrt{3}$，
不妨设P（x，y）（x＞0，y＞0）；
△F₁PF₂的面积S=$\frac{1}{2}$•|F₁F₂|•y=1，
即$\sqrt{3}$y=1，
故y=$\frac{\sqrt{3}}{3}$，代入$\frac{{x}^{2}}{4}$+y²=1解得，
x=$\frac{2\sqrt{6}}{3}$；
故$\overrightarrow{{PF}_{1}}$=（-$\sqrt{3}$-$\frac{2\sqrt{6}}{3}$，-$\frac{\sqrt{3}}{3}$），
$\overrightarrow{{PF}_{2}}$=（$\sqrt{3}$-$\frac{2\sqrt{6}}{3}$，-$\frac{\sqrt{3}}{3}$），
故$\overrightarrow{{PF}_{1}}$•$\overrightarrow{{PF}_{2}}$=（-$\sqrt{3}$-$\frac{2\sqrt{6}}{3}$）（$\sqrt{3}$-$\frac{2\sqrt{6}}{3}$）+（-$\frac{\sqrt{3}}{3}$）（-$\frac{\sqrt{3}}{3}$）
=$\frac{8}{3}$-3+$\frac{1}{3}$=0，
故答案为：0．

点评 本题考查了椭圆的简单性质的判断与应用，同时考查了平面向量的应用．