
| ���� ѧУ | Ը�� | ��Ը�� |
| AѧУ | 46 | 10 |
| BѧУ | 24 | 20 |
| P��K2��k�� | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
���� ��1���ɱ������ݿɵ�K2�Ĺ۲�ֵ�����ٽ�ֵ�Ƚϣ����ɵó����ۣ�
��2����ֱ�����ù�ʽ���ɵ���÷ֵ���ѧ������
��ֱ�����ù�ʽ���E��X����E��Y�������������ڱ��β����е÷֦ε���ѧ������
��� �⣺��1���ɱ������ݿɵ�K2�Ĺ۲�ֵ��$k=\frac{{100��{{��46��20-24��10��}^2}}}{70��30��44��56}��8.936$
��Ϊ8.936��6.635���������ڷ�����ĸ��ʲ�����0.01��ǰ������ΪԸ��μ�����������ѵ��ѧУ�йء���4�֣�
��2����������$E��S��=3��\frac{1}{6}+6��\frac{2}{6}+9��\frac{3}{6}=7$���֣�����6�֣�
�������Կ���ĸ���Ϊ�������X�����ȡ��5������������ȫ���ĸ���Ϊ�漴����Y��
��ȫ����Ϊ5-Y�������������У�X��B��8��0.8����Y���Ӳ���Ϊ8��4��5�ij����ηֲ���
���� E��X��=8��0.8=6.4��$E��Y��=\frac{4��5}{8}=2.5$����9�֣�
��Ϊ��=5X+12Y+7��5-Y��=5X+5Y+35������10�֣�
����E��=E��5X+5Y+35��=5E��X��+5E��Y��+35=79.5���֣�����12�֣�
���� ������Ҫ��������Լ���֪ʶ����������ɢ����������������뷽��Լ���ɢ�������������ֲ��У�ͬʱ�������������������������е��⣮


 ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�5] | B�� | [2��5] | C�� | [2��+�ޣ� | D�� | ��-�ޣ�2]��[5��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 24 | B�� | 28 | C�� | 32 | D�� | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
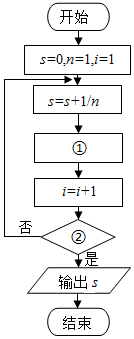 ��ͼ�������Ǽ���1+$\frac{1}{3}$+$\frac{1}{5}$+��+$\frac{1}{2015}$��ֵ��һ�������ͼ����ͼ��ִ�п��еĢٴ����жϿ��еĢڴ�Ӧ�������ǣ�������
��ͼ�������Ǽ���1+$\frac{1}{3}$+$\frac{1}{5}$+��+$\frac{1}{2015}$��ֵ��һ�������ͼ����ͼ��ִ�п��еĢٴ����жϿ��еĢڴ�Ӧ�������ǣ�������| A�� | n=n+1��i��1009 | B�� | n=n+2��i��1009 | C�� | n=n+1��i��1008 | D�� | n=n+2��i��1008 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com