Question

4．设x，y满足约束条件$\left\{\begin{array}{l}{x+y≥a}\\{x-y≤-1}\end{array}\right.$，且z=x+ay，则（　　）

• A． 当a＞0时有最大值
• B． 当a＞1时有最小值
• C． 当a＜0时有最大值
• D． 当0＜a＜1时有最小值

Answer 1

分析 对a的取值范围分类，分别作出可行域，由图形分析得到使目标函数有最值的a的范围得答案．

解答 解：若a＜0，由约束条件$\left\{\begin{array}{l}{x+y≥a}\\{x-y≤-1}\end{array}\right.$作出可行域如图，

化目标函数z=x+ay为$y=-\frac{1}{a}x+\frac{z}{a}$，
由图可知，当-1＜a＜0时，可行域内不存在使直线$y=-\frac{1}{a}x+\frac{z}{a}$在y轴上取得截距最小的点，则z=x+ay无最大值；
若0＜a＜1，由约束条件$\left\{\begin{array}{l}{x+y≥a}\\{x-y≤-1}\end{array}\right.$作出可行域如图，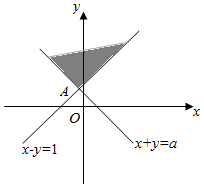

由图可知，当0＜a＜1时，可行域内不存在使直线$y=-\frac{1}{a}x+\frac{z}{a}$在y轴上取得截距最小的点，则z=x+ay无最小值；
若a＞1，由约束条件$\left\{\begin{array}{l}{x+y≥a}\\{x-y≤-1}\end{array}\right.$作出可行域如图，

由图可知，当直线$y=-\frac{1}{a}x+\frac{z}{a}$过A时，直线在y轴上的截距最小，z有最小值．
故选：B．

点评 本题考查了简单的线性规划，考查了数形结合的解题思想方法和分类讨论的数学思想方法，是中档题．