
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 可求出x≥0时函数f(x)的导数,根据导数符号便可判断该函数在[0,+∞)上的极值点个数,根据f(x)为偶函数关于y轴对称便可得出f(x)在(-∞,0)上的极值点个数,从而便可得出f(x)的极值点个数.
解答 解:x≥0时,f′(x)=-(2-x)4e1-x(7-x);
∴0≤x<2时,f′(x)<0,2<x<7时,f′(x)<0,x>7时,f′(x)>0;
∴x=7是f(x)在[0,+∞)上的极值点;
∵f(x)为偶函数,关于y轴对称;
∴x=-7为f(x)的又一个极值点;
∴f(x)的极值点个数为2.
故选B.
点评 考查基本初等函数、积的函数和复合函数的求导公式,以及极值点的定义及求法,偶函数的定义,偶函数图象的对称性.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某高中高一六班共有60名同学,学校为了解该班级数学科段考成绩的基本情况,将该班级所有同学的数学科段考成绩绘制频率分布直方图,其中成绩分布分组区间是:
某高中高一六班共有60名同学,学校为了解该班级数学科段考成绩的基本情况,将该班级所有同学的数学科段考成绩绘制频率分布直方图,其中成绩分布分组区间是:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-∞,-2) | C. | (2,+∞) | D. | (-∞,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
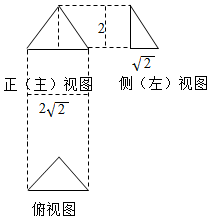 已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的体积为( )
已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的体积为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com