
已知三个集合A={a,b,c,d},B={m,n,p},C={x,y},在集合A,B,C中任取两个集合,然后从这两个集合中各选一个元素构成含有两个元素的集合,这种二元素的集合有多少个?
|
解 先分类,再分步.先分类,任取两个集合有三类情况,即选取: A,B;A,C;B,C.再对每一类分步考虑. (1)当选取的集合是A,B时,构成二元集可分两步完成,第一步从集合A中选取一个元素有4种方法,第二步再从集合B中选取一个元素有3种方法,根据乘法原理,可构成二元集合4×3个; (2)当选取的集合是A,C时,构成二元集合有4×2个; (3)当选取的集合为B,C时,构成的二元集合有3×2个, 根据加法原理,构成的二元集合共有 4×3+4×2+3×2=26(个). 注意,解决问题时,有时需用到加法原理,有时要用到乘法原理.而复杂问题一般先分类,各类中再分步,这就要同时用到加法原理与乘法原理.要确定解决问题时的分类标准及分步标准. |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2012年人教B版高中数学必修一1.2集合与集合的运算练习卷(一)(解析版) 题型:解答题
(本题满分12分)已知三个集合
A={x|x2-3x+2=0},B={x|x2-ax+(a-1)=0},C={x|x2-bx+2=0},问同时满足B 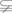 A、C
A、C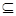 A的实数a、b是否存在?若存在,求出a、b所有值的集合;若不存在,请说明理由.
A的实数a、b是否存在?若存在,求出a、b所有值的集合;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013届辽宁省庄河市高二开学初考试理科数学试卷 题型:解答题
已知三个集合: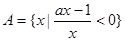 ,
,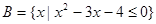 ,
, 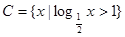 ,同时满足以下三个条件: 甲:
,同时满足以下三个条件: 甲: 为小于6的正整数;乙:A是B成立的充分不必要条件;丙:A是C成立的必要不充分条件,试确定数
为小于6的正整数;乙:A是B成立的充分不必要条件;丙:A是C成立的必要不充分条件,试确定数 。
。
查看答案和解析>>
科目:高中数学 来源:0123 月考题 题型:解答题
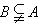 ,A∪C=A的实数a,b是否存在?若存在,求出实数a,b;若不存在,说明理由。
,A∪C=A的实数a,b是否存在?若存在,求出实数a,b;若不存在,说明理由。 查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com