
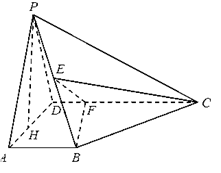
如图所示,在四棱锥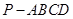 中,
中,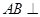 平面
平面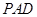 ,
,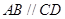 ,
,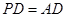 ,
,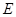 是
是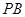 的中点,
的中点,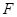 是
是 上的点且
上的点且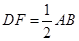 ,
,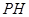 为△
为△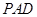 中
中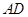 边上的高.
边上的高.
(1)证明: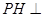 平面
平面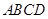 ;
;
(2)若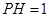 ,
,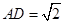 ,
,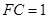 ,求三棱锥
,求三棱锥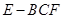 的体积;
的体积;
(3)证明: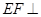 平面
平面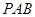 .
.
(1)见解析; (2)体积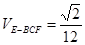 (3)见解析
(3)见解析
解析试题分析:(1)利用线面垂直的判断定理证明线面垂直,条件齐全.(2)利用棱锥的体积公式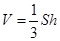 求体积.(3)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化.(4)在求三棱柱体积时,选择适当的底作为底面,这样体积容易计算.
求体积.(3)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化.(4)在求三棱柱体积时,选择适当的底作为底面,这样体积容易计算.
试题解析:(1)证明:因为 平面
平面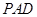 ,
,
所以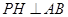 。
。
因为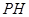 为△
为△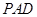 中
中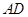 边上的高,
边上的高,
所以 。
。
因为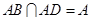 ,
,
所以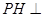 平面
平面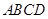 。 4分
。 4分
(2)连结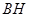 ,取
,取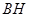 中点
中点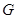 ,连结
,连结 。
。
因为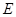 是
是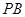 的中点,
的中点,
所以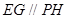 。
。
因为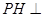 平面
平面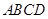 ,
,
所以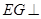 平面
平面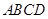 。
。
则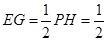 ,
,
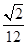 。 8分
。 8分
(3)证明:取 中点
中点 ,连结
,连结 ,
,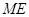 。
。
因为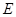 是
是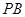 的中点, 所以
的中点, 所以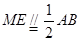 。
。
因为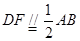 , 所以
, 所以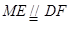 ,
,
所以四边形 是平行四边形,
是平行四边形,
所以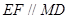 。
。
因为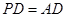 , 所以
, 所以 。
。
因为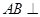 平面
平面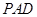 ,
,
所以 。
。
因为 , 所以
, 所以 平面
平面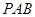 ,
,
所以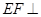 平面
平面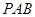 。 13分
。 13分
考点:(1)空间中线面垂直和平行的判定(2)几何体的体积.


科目:高中数学 来源: 题型:解答题
如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2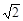 ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.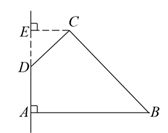
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知空间4个球,它们的半径分别为2, 2, 3, 3,每个球都与其他三个球外切,另有一个小球与这4个球都外切,则这个小球的半径为( )
A.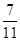 | B.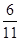 | C.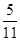 | D.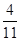 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图是某几何体的三视图,它的正视图和侧视图均为矩形,俯视图为正三角形(长度单位:cm)
(1)试说出该几何体是什么几何体;
(2)按实际尺寸画出该几何体的直观图,并求它的表面积及体积.(只要做出图形,不要求写作法)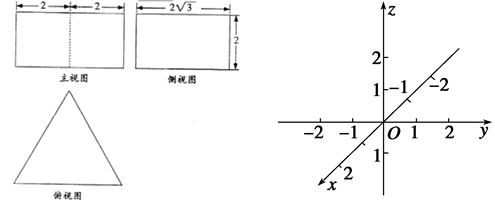
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知平面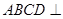 平面
平面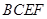 ,且四边形
,且四边形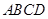 为矩形,四边形
为矩形,四边形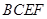 为直角梯形,
为直角梯形,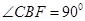 ,
,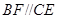 ,
,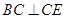 ,
,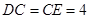 ,
,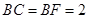 .
.
(1)作出这个几何体的三视图(不要求写作法).
(2)设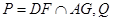 是直线
是直线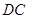 上的动点,判断并证明直线
上的动点,判断并证明直线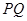 与直线
与直线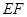 的位置关系.
的位置关系.
(3)求直线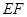 与平面
与平面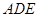 所成角的余弦值.
所成角的余弦值.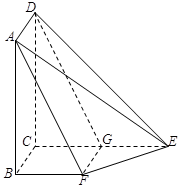
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
某师傅需用合板制作一个工作台,工作台由主体和附属
两部分组成,主体部分全封闭,附属部分是为了防止工件滑出
台面而设置的护墙,其大致形状的三视图如右图所示
(单位长度:  ), 则按图中尺寸,做成的工作台用去的合板的
), 则按图中尺寸,做成的工作台用去的合板的
面积为  。(制作过程合板损耗和合板厚度忽略不计)
。(制作过程合板损耗和合板厚度忽略不计)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com