Question

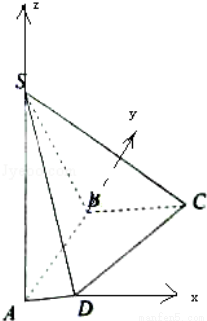
如图所示，在四棱锥S﹣ABCD中，底面ABCD是直角梯形，SA⊥平面ABCD，且AD∥BC，AB⊥AD，BC=2AD=2，AB=AS=．

（Ⅰ）求证：SB⊥BC；

（Ⅱ）求点A到平面SBC的距离；

（Ⅲ）求面SAB与面SCD所成二面角的大小．

 

 

Answer 1

【解析】

试题分析：

（Ⅰ）由线面垂直得SA⊥BC，从而得到BC⊥平面SAB，由此能证明SB⊥BC．

（Ⅱ）以A为原点，以AD为x轴，AB为y轴，AS为z轴，建立空间直角坐标系，利用向量法能求出点A到平面SBC的距离．

（Ⅲ）求出平面SAD的法向量和平面SAB的法向量利用向量法能求出面SAB与面SCD所成二面角的大小．

试题解析：（Ⅰ）证明：∵SA⊥平面ABCD，∴SA⊥BC，

又∵BC⊥AB，∴BC⊥平面SAB，

又SB?平面SAB，∴SB⊥BC．

（Ⅱ）【解析】
以A为原点，以AD为x轴，AB为y轴，AS为z轴，

建立空间直角坐标系，

由已知得S（0，0，），A（0，0，0），

B（0，，0），C（2，，0），D（0，0，1），

，

设平面SBC的法向量，

则，取y=1，得，

，

∴点A到平面SBC的距离d==．

（Ⅲ）【解析】
=（1，0，），，

设平面SAD的法向量，

则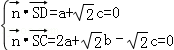，令c=1，得，

又平面SAB的法向量，

∴cos＜＞=，

∴面SAB与面SCD所成二面角的大小为45°．

考点：与二面角有关的立体几何综合题；直线与平面所成的角．