
如图,在五棱锥S—ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2, ,
,

(1) .
.
(2)证明:平面SBC⊥平面SAB.
(1)见解析; (2)见解析.
【解析】
试题分析:(1)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;(2)证明两个平面垂直,首先考虑直线与平面垂直,也可以简单记为“证面面垂直,找线面垂直”,是化归思想的体现,这种思想方法与空间中的平行关系的证明类似,掌握化归与转化思想方法是解决这类题的关键.
试题解析:(1)连结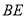 ,延长
,延长 交于点
交于点 ,则
,则 ,
,
∴ 为正三角形,∴
为正三角形,∴
又 ,∴
,∴ 因此,
因此,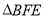 为正三角形,
为正三角形,
∴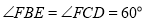 ,∴
,∴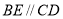

 .
.
(2)由题意, 为等腰三角形,
为等腰三角形,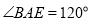 ,
,
∴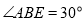 ,又
,又 ,
,
∴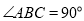 ,∴
,∴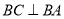
∵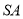 ⊥底面
⊥底面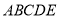 ,
,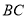
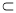 底面
底面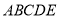 ,
,
∴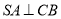 ,又
,又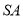
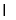
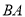
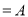 ,
,
∴ ⊥平面
⊥平面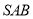 又
又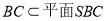
∴平面 ⊥平面
⊥平面 .
.
考点:(1)直线与平面平行的判定;(2)平面与平面垂直的判定.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源:2014-2015学年江西省南昌市高一上学期第一次考试数学试卷(解析版) 题型:解答题
(本题12分)函数 .
.
(1)若 ,求
,求 的值;
的值;
(2)确定函数 在区间
在区间 上的单调性,并用定义证明.
上的单调性,并用定义证明.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省高二上学期第一次月考文科数学试卷(解析版) 题型:解答题
(12分)若不等式组 (其中
(其中 )表示的平面区域的面积是9.
)表示的平面区域的面积是9.
(1)求 的值;
的值;
(2)求 的最小值,及此时
的最小值,及此时 与
与 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2015届内蒙古赤峰市高二下学期期末理科数学试卷(解析版) 题型:解答题
已知函数f(x)=|x+a|+|x﹣2|
(1)当a=﹣3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x﹣4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届内蒙古赤峰市高二下学期期末理科数学试卷(解析版) 题型:解答题
如图所示,在四棱锥S﹣ABCD中,底面ABCD是直角梯形,SA⊥平面ABCD,且AD∥BC,AB⊥AD,BC=2AD=2,AB=AS= .
.
(Ⅰ)求证:SB⊥BC;
(Ⅱ)求点A到平面SBC的距离;
(Ⅲ)求面SAB与面SCD所成二面角的大小.

查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省高邮市高二九月月考数学试卷(解析版) 题型:填空题
 为异面直线,且
为异面直线,且 所成角为40°,直线c与
所成角为40°,直线c与 均异面,且所成角均为θ,若这样的c共有四条,则θ的范围为 .
均异面,且所成角均为θ,若这样的c共有四条,则θ的范围为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com