练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    正方体ABCD﹣A1B1C1D1的棱长为1，若动点P在线段BD1上运动，则的取值范围是　　．

    考点：

    平面向量数量积的运算．

    专题：

    平面向量及应用．

    分析：

    建立空间直角坐标系，求出有关点的坐标可得、、、的坐标，再由 =1﹣λ∈[0，1]，可得的取值范围．

    解答：

    解：以所在的直线为x轴，以所在的直线为y轴，以所在的直线为z轴，建立空间直角坐标系．

    则D（0，0，0）、C（0，1，0）、A（1，0，0）、B（1，1，0）、D1（0，0，1）．

    ∴=（0，1，0）、 （﹣1，﹣1，1）．

    ∵点P在线段BD1上运动，∴=λ•=（﹣λ，﹣λ，λ），且0≤λ≤1．

    ∴=+=+=（﹣λ，1﹣λ，λ），

    ∴=1﹣λ∈[0，1]，

    故答案为[0，1]．

    点评：

    本题主要考查两个向量坐标形式的运算，两个向量的数量积公式，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    两球O1和O2在棱长为1的正方体ABCD-A1B1C1D1的内部，且互相外切，若球O1与过点A的正方体的三个面相切，球O2与过点C1的正方体的三个面相切，则球O1和O2的表面积之和的最小值为（　　）
    A、(6-3
    		3
    )π
    B、(8-4
    		3
    )π
    C、(6+3
    		3
    )π
    D、(8+4
    		3
    )π

    查看答案和解析>>

    科目：高中数学 来源： 题型：

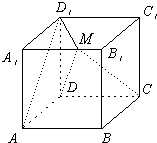    如图，正方体ABCD-A1B1C1D1的棱长为6，动点M在棱A1B1上．
    （1）求证：DM⊥AD1；
    （2）当M为A1B1的中点时，求CM与平面DC1所成角的正弦值；
    （3）当A1M=
    34
    A1B1时，求点C到平面D1DM的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下面四个计算题中，结果正确的是
    ①②③
    ①②③
    ．（填序号）
    ①若|
    a
    |=2，|
    b
    |=3    ，且
    a
    与
    b
    的夹角为600，则|
    a
    -
    b
    |=
    		7
    ；
    ②棱长为2正方体ABCD-A1B1C1D1中，点A到平面BDD1B1的距离为d，则d=
    		2
    ；
    ③棱长都是1的平行六面体ABCD-A1B1C1D1中，∠BAD=∠BAA1=∠DAA1=600，则对角线的长AC1=
    		6
    ；
    ④在1200的二面角α-AB-β中AC?α，BD?β，AB⊥AC，AB⊥BD，AB=AC=BD=1，则点C与D的距离CD=
    		2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•北京）如图，在正方体ABCD-A1B1C1D1中，P为对角线BD1的三等分点，P到各顶点的距离的不同取值有（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在正方体ABCD-A1B1C1D1中，异面直线BC1与AB1所成角的大小为（　　）
    A、
    π
    2
    B、
    π
    3
    C、
    π
    4
    D、
    π
    6

    查看答案和解析>>

    同步练习册答案