
分析 (1)由一元二次方程的解法求出对应方程的根,由一元二次不等式的解法求出不等式的解集;
(2)先化简不等式,由一元二次方程的解法求出对应方程的根,由一元二次不等式的解法求出不等式的解集;
(3)先化简分式不等式,再等价转化为一元二次不等式组,由一元二次不等式的解法求出不等式的解集;
(4)先化简分式不等式,再等价转化为对应不等式组,由穿根法求出高次不等式的解集.
解答 解:(1)由6x2-x-1=0得(3x+1)(2x-1)=0,
解得x=$-\frac{1}{3}$ 或x=$\frac{1}{2}$,…2
所以不等式6x2-x-1≥0 的解集为{x|x$≤-\frac{1}{3}$或x$≥\frac{1}{2}$}…4
(2)由-x2+2x-$\frac{2}{3}$>0得3x2-6x+2<0,
因为3>0,且方程3x2-6x+2=0的解是:x1=$1-\frac{\sqrt{3}}{3}$,x2=$1+\frac{\sqrt{3}}{3}$,
所以原不等式的解集是 {x|$1-\frac{\sqrt{3}}{3}<x<1+\frac{\sqrt{3}}{3}$}…8
(3)由$\frac{x+1}{2-x}≥3$得$\frac{x+1}{2-x}-3≥0$,则$\frac{x+1-3(2-x)}{2-x}≥0$,即$\frac{4x-5}{2-x}≥0$,
所以$\left\{\begin{array}{l}{(4x-5)(x-2)≤0}\\{x-2≠0}\end{array}\right.$,解得$\frac{5}{4}≤x<2$,
则不等式的解集是{x|$\frac{5}{4}≤x<2$}…12
(4)原不等式化为:$\frac{3{x}^{2}-14x+14}{{x}^{2}-6x+8}-1≥0$,
整理得$\frac{(x-1)(x-3)}{(x-2)(x-4)}≥$ 0
即$\left\{\begin{array}{l}{(x-1)(x-2)(x-3)(x-4)≥0}\\{x-2≠0且x-4≠0}\end{array}\right.$,如图
所以原不等式的解集为{x|x≤1或2<x≤3或x>4}…16
点评 本题考查了分式不等式的化简以及等价转化,一元二次不等式的解法,以及穿根法求高次不等式的解集,考查转化思想,化简、变形能力.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{2}{15}$ | C. | $\frac{5}{36}$ | D. | $\frac{3}{20}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | an=3n-1 | B. | an=2n-1 | C. | an=3n | D. | an=2n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n=4,p=0.6 | B. | n=6,p=0.4 | C. | n=8,p=0.3 | D. | n=24,p=0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
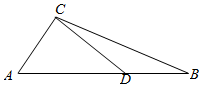 在△ABC中,内角A、B、C的对边分别是a、b、c,且b2+c2-a2=bc,且∠BDC=135°,AC=2$\sqrt{3}$,DB=3.
在△ABC中,内角A、B、C的对边分别是a、b、c,且b2+c2-a2=bc,且∠BDC=135°,AC=2$\sqrt{3}$,DB=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com