
 .
. ,纵坐标不变,继而将所得图象上的各点向右平移
,纵坐标不变,继而将所得图象上的各点向右平移 个单位,得到函数y=g(x)的图象,求函数g(x)的单调递增区间;
个单位,得到函数y=g(x)的图象,求函数g(x)的单调递增区间; 的值.
的值.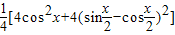 =sinx,根据函数的图象变换法则可求g(x)=
=sinx,根据函数的图象变换法则可求g(x)=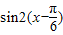 =
=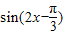 ,令
,令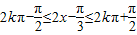 ,k∈Z可求g(x)的单调递增区间
,k∈Z可求g(x)的单调递增区间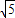 ,由余弦定理可求cosA=
,由余弦定理可求cosA=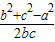 ,进而可求cos2A=2cos2A-1,利用sin2A=
,进而可求cos2A=2cos2A-1,利用sin2A=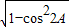 可求sin2A,然后由两角和的余弦公式可求
可求sin2A,然后由两角和的余弦公式可求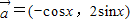 ,
,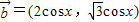
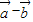 =
=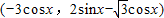
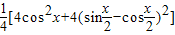
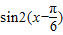 =
=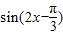 (4分)
(4分)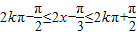 ,k∈Z
,k∈Z ,k∈Z
,k∈Z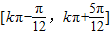 ,k∈Z
,k∈Z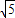 (7分)
(7分)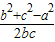 =
=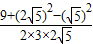 =
=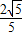 (8分)
(8分)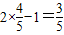 (9分)
(9分)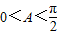 ,0<2A<π,所以sin2A>0
,0<2A<π,所以sin2A>0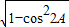 =
= (10分)
(10分)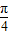 )=
)=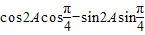
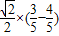 =
=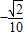 (12分)
(12分)

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
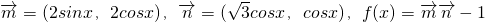 .
. ,把所得到的图象再向左平移
,把所得到的图象再向左平移 单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
单位,得到函数y=g(x)的图象,求函数y=g(x)在区间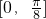 上的最小值.
上的最小值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年内蒙古乌兰察布市集宁一中高三(上)第六次周考数学试卷(解析版) 题型:解答题
 .
. ,把所得到的图象再向左平移
,把所得到的图象再向左平移 单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
单位,得到函数y=g(x)的图象,求函数y=g(x)在区间 上的最小值.
上的最小值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省枣庄市高三(上)期中数学试卷(理科)(解析版) 题型:解答题
 .
. ,纵坐标不变,继而将所得图象上的各点向右平移
,纵坐标不变,继而将所得图象上的各点向右平移 个单位,得到函数y=g(x)的图象,求函数g(x)的单调递增区间;
个单位,得到函数y=g(x)的图象,求函数g(x)的单调递增区间;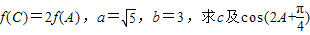 的值.
的值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市崇明县建设中学高三(下)摸底数学试卷(解析版) 题型:解答题
 .
. ,把所得到的图象再向左平移
,把所得到的图象再向左平移 单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
单位,得到函数y=g(x)的图象,求函数y=g(x)在区间 上的最小值.
上的最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com