
| A. | 命题“若x2-5x+6=0,则x=2”的逆否命题是“若x≠2,则x2-5x+6≠0” | |
| B. | 命题“角α的终边在第一象限,则α是锐角”的逆命题为真命题 | |
| C. | 已知命题p和q,若p∨q为假命题,则命题p与q中必一真一假 | |
| D. | 命题“若x>y,则x>|y|”的逆命题是真命题 |
分析 写出命题“若x2-5x+6=0,则x=2”的逆否命题,判断A正确;
写出命题“角α的终边在第一象限,则α是锐角”的逆命题,并判断真假性;
根据复合命题的真假性判断C错误;
写出命题“若x>y,则x>|y|”的逆命题,并判断真假性.
解答 解:对于A,命题“若x2-5x+6=0,则x=2”的逆否命题是
“若x≠2,则x2-5x+6≠0”,故A正确;
对于B,命题“角α的终边在第一象限,则α是锐角”的逆命题是
“角α是锐角,则角α的终边在第一象限”,它是真命题,故B正确;
对于C,若命题p∨q为假命题,则命题p与q一真一假或都为假命题,故C错误;
对于D,命题“若x>y,则x>|y|”的逆命题是:
“若x>|y|,则x>y”,它是真命题,故D正确.
故选:C.
点评 本题考查了命题真假性的判断问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
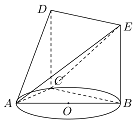 如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,已知AE与平面ABC所成的角为θ,且$tanθ=\frac{{\sqrt{3}}}{2}$;
如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,已知AE与平面ABC所成的角为θ,且$tanθ=\frac{{\sqrt{3}}}{2}$;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,0)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-2,0)∪(0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{3}{2}$]∪[$\frac{3}{2}$,+∞) | B. | (-∞,-3]∪[$\frac{3}{2}$,+∞) | C. | (-∞,-3]∪[$\frac{5}{2}$,+∞) | D. | (-∞,-$\frac{3}{2}$]∪[$\frac{5}{2}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com