
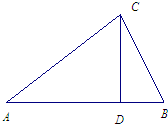
 如图,△ABC是某屋顶的断面,CD⊥AB,横梁AB的长是竖梁CD长的2倍.设计时应使y=tanA+2tanB保持最小,试确定D点的位置,并求y的最小值.
如图,△ABC是某屋顶的断面,CD⊥AB,横梁AB的长是竖梁CD长的2倍.设计时应使y=tanA+2tanB保持最小,试确定D点的位置,并求y的最小值. =
= ,Rt△BCD中,tanB=
,Rt△BCD中,tanB= =
=

 =
=
 ;当且仅当
;当且仅当 时取等号
时取等号 时,y取得最小值
时,y取得最小值
 ,
,
 时,y有最小值
时,y有最小值
 且tgB=
且tgB= ,代入y=tanA+2tanB的表达式,再进行配凑,得到y=
,代入y=tanA+2tanB的表达式,再进行配凑,得到y= ,最后通过基本不等式讨论分母的最小值,可得y的最小值是
,最后通过基本不等式讨论分母的最小值,可得y的最小值是 .根据取等号的条件得到:当且仅当
.根据取等号的条件得到:当且仅当 时,取到这个最小值,求出AD与DB的比值,从而确定D点的位置,问题得到解决.
时,取到这个最小值,求出AD与DB的比值,从而确定D点的位置,问题得到解决.

科目:高中数学 来源: 题型:
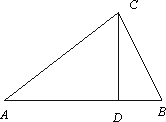
 如图,△ABC是某屋顶的断面,CD⊥AB,横梁AB的长是竖梁CD长的2倍.设计时应使y=tanA+2tanB保持最小,试确定D点的位置,并求y的最小值.
如图,△ABC是某屋顶的断面,CD⊥AB,横梁AB的长是竖梁CD长的2倍.设计时应使y=tanA+2tanB保持最小,试确定D点的位置,并求y的最小值.查看答案和解析>>
科目:高中数学 来源:河南省信阳市商城高中2006-2007学年度高三数学单元测试、不等式二 题型:044
解答题:解答应写出文字说明,证明过程或演算步骤.
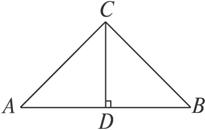
如图,△ABC是某屋顶的断面,CD⊥AB,横梁AB的长是竖梁CD长的2倍.设计时应使![]() 保持最小,试确定D点的位置,并求y的最小值.
保持最小,试确定D点的位置,并求y的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010年广东省广州一中高三数学二轮复习:不等式(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com