
段论:“①雅安人一定坚强不屈;②雅安人是中国人;③所有的中国人都坚强不屈”中,其中“大前提”和“小前提”分别是等于( )
| A.①② | B.③① | C.③② | D.②③ |
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:单选题
用反证法证明命题:“若整系数一元二次方程 有有理根,那么
有有理根,那么 中至少有一个是偶数时,下列假设中正确的是
中至少有一个是偶数时,下列假设中正确的是
A.假设 都是偶数 都是偶数 |
B.假设 都不是偶数 都不是偶数 |
C.假设 至多有一个是偶数 至多有一个是偶数 |
D.假设 至多有两个是偶数 至多有两个是偶数 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用反证法证明命题:“若a,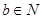 ,
,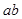 能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
| A.a,b都能被5整除 | B.a,b都不能被5整除 |
| C.a,b有一个能被5整除 | D.a,b有一个不能被5整除 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用数学归纳法证明1+2+3+…+(2n+1)=(n+1)(2n+1)时,从n=k到n=k+1,左边需增添的代数式是( )
| A.2k+2 | B.2k+3 |
| C.2k+1 | D.(2k+2)+(2k+3) |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
给出下面类比推理命题(其中Q为有理数集,R为实数集,C为复数集):
①“若a,b∈R,则a-b=0⇒a=b”,类比推出“若a,b∈C,则a-b=0⇒a=b”;
②“若a,b,c,d∈R,则复数a+bi=c+di⇒a=c,b=d”,类比推出,“若a,b,c,d∈Q,则a+b =c+d
=c+d ⇒a=c,b=d”;
⇒a=c,b=d”;
③“若a,b∈R,则a-b>0⇒a>b”,类比推出“若a,b∈C,则a-b>0⇒a>b”;
④“若x∈R,则|x|<1⇒-1<x<1”,类比推出“若z∈C,则|z|<1⇒-1<z<1”.
其中类比正确的为( )
| A.①② | B.①④ | C.①②③ | D.②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com