练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    用反证法证明命题：“若整系数一元二次方程有有理根，那么中至少有一个是偶数时，下列假设中正确的是

    A．假设都是偶数
    B．假设都不是偶数
    C．假设至多有一个是偶数
    D．假设至多有两个是偶数

    B

    解析试题分析：用反证法法证明数学命题时，应先假设要证的命题的反面成立，即要证的命题的否定成立，而命题：“若整数系数一元二次方程ax2+bx+c=0（a≠0）有有理根，则a，b，c中至少有一个是偶数”的否定为：“假设a，b，c都不是偶数”，故选：B．
    考点：反证法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：单选题

    用数学归纳法证明“时，从“到”时，左边应增添的式子是（    ）．

    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    用反证法证明命题：“三角形的内角中至少有一个不大于60度”时，反设正确的是（   ）

    A．假设三内角都不大于60度
    B．假设三内角都大于60度
    C．假设三内角至多有一个大于60度
    D．假设三内角至多有两个大于60度

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    用反证法证明命题“三角形的内角至多有一个钝角”时，假设的内容应为（ ）

    A．假设至少有一个钝角 B．假设至少有两个钝角 
    C．假设没有一个钝角 D．假设没有一个钝角或至少有两个钝角 

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    用三段论推理命题：“任何实数的平方大于0，因为a是实数，所以a2>0”，你认为这个推理(   )

    A．大前题错误B．小前题错误C．推理形式错误 D．是正确的

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    段论：“①雅安人一定坚强不屈；②雅安人是中国人；③所有的中国人都坚强不屈”中，其中“大前提”和“小前提”分别是等于（   ）

    A．①②B．③①C．③②D．②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    由“正三角形的内切圆切于三边的中点”可类比猜想：正四面体的内切球切于四个面(　　)

    A．各正三角形内一点 B．各正三角形的某高线上的点
    C．各正三角形的中心 D．各正三角形外的某点

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    如图所示程序图运行的结果是     ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    用反证法证明命题“设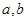为实数，则方程至少有一个实根”时，要做的假设是（   ）

    A．方程没有实根 B．方程至多有一个实根
    C．方程至多有两个实根 D．方程恰好有两个实根

    查看答案和解析>>

    同步练习册答案