
函数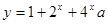 在
在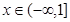 上
上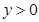 恒成立,则
恒成立,则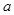 的取值范围是
的取值范围是 .
.
科目:高中数学 来源: 题型:
给出定义:若函数![]() 在
在![]() 上可导,即
上可导,即![]() 存在,且导函数
存在,且导函数![]() 在
在![]() 上也可导,则称
上也可导,则称![]() 在
在![]() 上存在二阶导函数,记
上存在二阶导函数,记![]() ,若
,若![]() 在
在![]() 上恒成立,则称
上恒成立,则称![]() 在
在![]() 上为凸函数。以下四个函数在
上为凸函数。以下四个函数在![]() 上不是凸函数的是( )
上不是凸函数的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数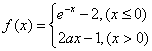 (
(![]() 是常数且
是常数且![]() ).对于下列命题:
).对于下列命题:
①函数![]() 的最小值是
的最小值是![]() ;②函数
;②函数![]() 在
在![]() 上是单调函数;③若
上是单调函数;③若![]() 在
在![]() 上恒成立,则
上恒成立,则![]() 的取值范围是
的取值范围是![]() ;④对任意
;④对任意![]() 且
且![]() ,恒有
,恒有![]() .
.
其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省高三上学期期末理科数学试卷 题型:选择题
已知函数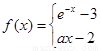
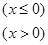 (
(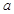 为常数且
为常数且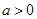 ),对于下列结论
),对于下列结论
①函数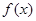 的最小值为
的最小值为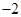 ,②函数
,②函数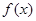 在
在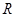 上是单调函数,③若
上是单调函数,③若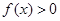 在
在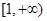 上恒成立,则
上恒成立,则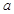 的取值范围为
的取值范围为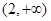 ,④当
,④当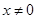 时,
时,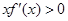 (这里
(这里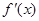 是
是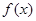 的导函数),其中正确的是( )
的导函数),其中正确的是( )
A.①③④ B.①②③ C.①④ D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com