【题目】已知双曲线
过点
且渐近线为
，则下列结论错误的是（ ）
A.曲线的方程为
；
B.左焦点到一条渐近线距离为
；
C.直线
与曲线有两个公共点；
D.过右焦点截双曲线所得弦长为
的直线只有三条；
【答案】C
【解析】
求出双曲线的标准方程，根据方程判断双曲线的性质．B直接求出左焦点到渐近线的距离，C由直线方程与双曲线方程联立求得公共点坐标，D考虑到过焦点，因此一是求出通径长，一是求出实轴长，与它们比较可得．
因为双曲线的渐近线方程为
，所以可设双曲线方程为
，又双曲线过点
，所以
，所以双曲线方程为
，A正确；
由双曲线方程知
，
，左焦点为
，渐近线方程为
，左焦点到渐近线的中庸为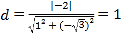
，B正确；
由
得
，代入双曲线方程整理得
，解得
，所以
，直线与双曲线只有一个公共点
，C错；
双曲线的通径长为
，因此过右焦点，且两顶点都右支上弦长为
的弦有两条，又两顶点间距离为
，因此端点在双曲线左右两支上且弦长为的弦只有一条，为实轴，所以共有3条弦的弦长为，D正确．
故选：C．
冲刺100分1号卷系列答案科目：高中数学 来源： 题型：
【题目】现有如下命题：①若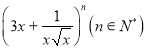
的展开式中含有常数项，且
的最小值为
；②
；③若有一个不透明的袋子内装有大小、质量相同的
个小球，其中红球有
个，白球有
个，每次取一个，取后放回，连续取三次，设随机变量
表示取出白球的次数，则
；④若定义在R上的函数
满足
，则的最小正周期为
；
则正确论断有______________.（填写序号）
查看答案和解析>>
科目：高中数学 来源： 题型：
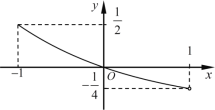
【题目】函数
的定义域为
，其图象如图所示．函数
是定义域为
的奇函数，满足
，且当
时，
．给出下列三个结论：
①
；
②函数在
内有且仅有
个零点；
③不等式
的解集为
．
其中，正确结论的序号是________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为响应党的号召，坚决打赢脱贫攻坚战，某地区实行了帮扶单位定点帮扶扶贫村脱贫.为了解该地区贫困户对其所提供的帮扶的满意度，随机调查了40个贫困户，得到贫困户的满意度评分如下：
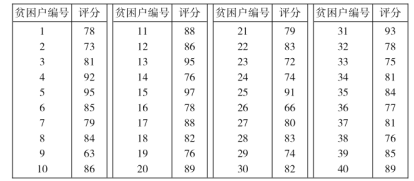
现按贫困户编号从小到大的顺序分组，用系统抽样法从40名贫困户中抽取容量为10的样本.
（1）若在第一分段里随机抽到的第一个样本的评分数据为81，记第二和第十个样本的评分数据分别为a，b，请写出a，b的值；
（2）若10个样本的评分数据分别为92，84，86，78，89，74，83，78，77，89.请你计算所抽到的10个样本的平均数
和方差
；
（3）在（1）条件下，若贫困户的满意度评分在
之间，则满意度等级为“A级”.试应用样本估计总体的思想，用（2）中的样本数据，估计在满意度为“A级”的贫困户中随机地抽取2户，所抽到2户的满意度评分均“超过80”的概率.
（参考数据：
，
，
）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某企业生产甲、乙两种产品均需用A，B两种原料，已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获利润分别为3万元、4万元，则该企业每天可获得的最大利润为（ ）
甲 | 乙 | 原料限额 | |
A/吨 | 3 | 2 | 12 |
B/吨 | 1 | 2 | 8 |
A.15万元B.16万元C.17万元D.18万元
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在三棱锥P﹣ABC中，平面PBC⊥平面ABC，∠ACB＝90°，BC＝PC＝2，若AC＝PB，则三棱锥P﹣ABC体积的最大值为（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对两个变量
与
进行线性相关性和回归效果分析，得到一组样本数据：
、
、
、
，则下列说法不正确的是（ ）
A.残差平方和越小的模型，拟合的效果越好
B.由样本数据利用最小二乘法得到的回归方程表示的直线必过样本点的中心
C.若变量与之间的相关系数
，则变量与之间具有很强的线性相关性
D.用相关指数
来刻画回归效果，越小，说明模型的拟合效果越好
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图是一“T”型水渠的平面视图（俯视图），水渠的南北方向和东西方向轴截面均为矩形，南北向渠宽为4m，东西向渠宽
m（从拐角处，即图中
，
处开始）．假定渠内的水面始终保持水平位置（即无高度差）．
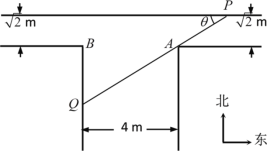
（1）在水平面内，过点的一条直线与水渠的内壁交于
，
两点，且与水渠的一边的夹角为
，将线段
的长度
表示为
的函数；
（2）若从南面漂来一根长为7m的笔直的竹竿（粗细不计），竹竿始终浮于水平面内，且不发生形变，问：这根竹竿能否从拐角处一直漂向东西向的水渠（不会卡住）？请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
