
分析 由题意可得A=$\sqrt{2}$,$\sqrt{2}$sin(2ω+φ)=$\sqrt{2}$,解得:sin(2ω+φ)=1,①由$\sqrt{2}$sinφ=1,解得φ=$\frac{π}{4}$或$\frac{3π}{4}$,讨论由①解得ω=k$π±\frac{π}{8}$,k∈Z②,由T=$\frac{2π}{ω}$>4,解得:0<$ω<\frac{π}{2}$或0<ω<π,从而解得ω,φ的值,即可求得解析式.
解答 解:∵在右侧的第一个最大值点为(2,$\sqrt{2}$).
∴A=$\sqrt{2}$,$\sqrt{2}$sin(2ω+φ)=$\sqrt{2}$,解得:sin(2ω+φ)=1,①
∵函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<2π)的图象在y轴上的截距为1,
∴函数图象过(0,1),
∴$\sqrt{2}$sinφ=1,
∵0<φ<2π,
∴φ=$\frac{π}{4}$或$\frac{3π}{4}$,
∴由①可得:sin(2ω+$\frac{π}{4}$)=1,或sin(2ω+$\frac{3π}{4}$)=1,解得:ω=k$π±\frac{π}{8}$,k∈Z②,
∵由题意可得:T=$\frac{2π}{ω}$>2(2-0)=4,或$\frac{2π}{ω}$>2,解得:0<$ω<\frac{π}{2}$,0<ω<π
∴由②解得:ω=$\frac{π}{8}$或$\frac{7π}{8}$,故φ=$\frac{π}{4}$,
∴函数的解析式为:y=$\sqrt{2}$sin($\frac{π}{8}$x+$\frac{π}{4}$)或y=$\sqrt{2}$sin($\frac{7π}{8}$x+$\frac{π}{4}$).
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查了正弦函数的图象和性质,考查了分类讨论思想的应用,属于基本知识的考查.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | (-∞,$\frac{1}{2}$)∪(1,+∞) | C. | ($\frac{1}{2},1$) | D. | [0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
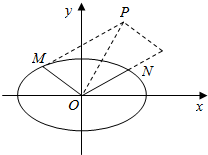 如图所示,已知M,N是椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}$=1上两动点,且直线OM与ON的斜率之积为-$\frac{1}{2}$(其中O为坐标原点),若点P满足$\overrightarrow{OP}$=$\overrightarrow{OM}$+2$\overrightarrow{ON}$.问:是否存在两个定点F1,F2,使得|PF1|+|PF2|为定值.若存在,求F1,F2的坐标;若不存在,说明理由.
如图所示,已知M,N是椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}$=1上两动点,且直线OM与ON的斜率之积为-$\frac{1}{2}$(其中O为坐标原点),若点P满足$\overrightarrow{OP}$=$\overrightarrow{OM}$+2$\overrightarrow{ON}$.问:是否存在两个定点F1,F2,使得|PF1|+|PF2|为定值.若存在,求F1,F2的坐标;若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com